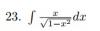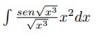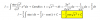Observa que se trata de encontrar un cero de la función cuya expresión es: f(x) = x^7 - 127, cuya derivada tiene la expresión: f ' (x) = 7x^6.

Observa que tenemos:

f(1) = - 126 < 0, y f(2) = 1 > 0, por lo que sabemos que el cero de la función pertenece al intervalo (1,2);

luego evaluamos la expresión de la derivada segunda de la función para estos dos valores:

f ' ' (1) = 7 > 0, y f ' ' (2) = 448 > 0;

luego, observa que la condición de Fourier: f(xo)*f ' ' (xo) > 0, se cumple para: xo = 2.

Luego, planteamos la fórmula recursiva y tenemos:

x1 = xo - ( xo^7 - 127 ) / 7xo^6 = 2 - (128 - 127)/448 = 2 - 1/448 = 895/448 = 1,9977678571....

x2 = x1 - ( x1^7 - 127 ) / 7x1^6 = ... queda para que hagas los cálculos, hasta obtener la cantidad de cifras decimales exactas con las que necesitas aproximar.

Espero haberte ayudado.

La idea del planteo por el método de las partes es correcta, pero debes corregir:

u = 2x+3, de donde tienes: du = 2dx (aquí se trata de un problema de notación sólamente);

dv = sen(5x)dx, de donde tienes: v = (-1/5)cos(5x) (aquí se trata de la notación en el diferencial, y del planteo de la expresión de la función primitiva).

Luego puedes continuar la tarea.

Espero haberte ayudado.

Foto del enunciado original, por favor.

Si el argumento en ambas raíces cuartas (indicamo con (4V)) es (3x+1), observa que puedes hacer pasaje de término, resuelves a la izquierda y queda:

2 * (4V)(3x+1) = 4, luego multiplicas en ambos miembros de la ecuación por 1/2 y queda:

(4V)(3x+1) = 2, luego haces pasaje de raíz como potencia y queda:

3x + 1 = 2^4, resuelves a la derecha, haces pasaje de término, vuelves a resolver y queda:

3x = 15, luego haces pasaje de factor como divisor, resuelves a la derecha y llegas a:

x = 5, que es una solución válida como puedes probar reemplazando en la ecuación inicial

Espero haberte ayudado.

Muchas gracias!! :)

Puedes plantear la sustitución (cambio de variable): w = 1 - x^2 (*), de donde tienes: dw = -2xdx, y luego tienes: (-1/2)dw = xdx, luego sustituyes y la integral queda:

I = ∫ ( 1/V(w) )*(-1/2)*dw = extraemos factor constante y expresamos a la raíz como potencia:

= (-½) ∫ w^(-½)*dw = integramos:

= (-½)*w^(½) / ½ + C = simplificamos en el primer término:

= - w^(½) + C = volvemos a sustituir a partir de la ecuación señaada (*):

= - (1 - x^2)^(½) + C = escribimos la potencia como raíz:

= -V(1 - x^2) + C.

Espero haberte ayudado.

Así, Carlos: 

Comencemos con la sustitución: w = x³ (*), de donde tienes: dw = 3x²dx, y luego: (1/3)dw = x²dx, luego sustituyes y la integral queda:

I = ∫ ( sen( V(w) ) / V(w) )*(1/3)dw = extraemos factor constante y ordenamos factores en la expresión de la función:

= (⅓) ∫ sen( V(w) )*( 1 / V(w) )*dw =

aplicamos una nueva sustitución: w = t², de donde tienes: V(w) = t (**), tamibén tienes: dw = 2tdt, luego sustituyes y la integral queda:

I = (⅓) ∫ sent * (1/t) * 2tdt = extraemos y resolvemos factores constantes, simplificamos en la expresión de la función, y la integral queda:

I = (⅔) ∫ sentdt = integramos = (⅔)(-cost) + C = (- ⅔)cost + C,

luego aplicamos la sustitución indicada (**) y queda:

I = (- ⅔)cos( V(w) ) + C,

luego aplicamos la sustitución indicada (*) y llegamos a:

I = (- ⅔)cos( V(x³) ) + C.

Espero haberte ayudado.

Revisa las operaciones, Alicia. El procedimiento es correcto:

Observa que a partir de la primera ecuación tienes: b = (2/3)a, y que a partir de la segunda tienes: c = (4/5)a, luego puedes plantear la fórmula del coseno:

a² = b² + c² - 2bc*cosA, luego sustituyes las expresiones para b y c, resuelves los cuadrados y queda:

a² = (4/9)a² + (16/25)a² - 2(2/3)(4/5)a², luego simplificamos el factor común a² (asumimos que no es igual a cero), resolvemos en el último término y queda:

1 = 4/9 + 16/25 - (16/15)cosA, hacemos pasajes de términos, resolvemos a la derecha y queda:

(16/15)cosA = 19/225, hacemos pasaje de factor como divisor, resolvemos a la derecha y queda:

cosA = 19/240.

Luego, puedes aplicar la identidad trigonométrica: cos(A/2) = V( (1 + cosA)/2 ) y completar el cálculo.

Espero haberte ayudado.

Comencemos con el primer miembro:

senx + tanx = senx + senx/cosx = extraemos denominador común = (senxcosx + senx)/cosx, luego la ecuación queda:

(senxcosx + senx)/cosx = 3cosxsenx, hacemos pasaje de divisor como factor y queda:

senxcosx + senx = 3senx(cosx)^2, hacemos pasaje de término y queda:

senxcosx + senx - 3senx(cosx)^2 = 0, extraemos factor común y queda:

senx( cosx + 1 - 3(cosx)^2 ) = 0, luego por anulación de un producto tenemos dos opciones:

a) senx = 0, componemos con la función inversa del seno y queda:

x1 = 0, pi,  2pi, ... (en general: x1 = kpi, con k ∈ Z.

b) cosx + 1 - 3(cosx)^2 = 0, planteamos la sustitución (cambio de incógnita) w = cosx (*) y queda:

w + 1 - 3w^2 = 0, multiplicamos por -1 en todos los términos de la ecuación, ordenamos términos y queda:

3w^2 - w - 1 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y quedan las soluciones:

b1) w = ( 1 + V(13) )/6 = 0,768 (aproximadamente);

b2) w = ( 1 - V(13) )/6 = -0,434 (aproximadamente).

Para cada opción, volvemos a la ecuación de la sustitución señalada (*) y quedan:

b1) cosx = 0,768 (observa que corresponde a valores del primer y del cuarto cuadrante), componemos con la función inversa del coseno y quedan dos opciones;

x2 = 39,83° = 0,695 rad (en general: x2 = 0,695 + 2kpi, con k ∈ Z);

x3 = 360° - 39,83° = 320,17° = 5,588 rad (en general: x3 = 5,588 + 2kpi, con k ∈ Z).

b2) cosx = -0,434 (observa que corresponde a valores del segundo y del tercer cuadrante), componemos con la función inversa del coseno y quedan dos opciones:

x4 = 115,72° = 2,020 rad (en general: x4 = 2,020 + 2kpi, con k ∈ Z);

x5 =  244,28° = 4,263 rad (en general: x5 = 4,263 + 2kpi, con k ∈ Z).

Espero haberte ayudado.

Plantea la sustitución (cambio de variable): t = 3x^2, de donde tienes: dt = 6x*dx, y luego tienes: (1/6)dt = x*dx, luego sustituyes y la integral queda:

I = ∫ e^t *(1/6)*dt = (1/6) * ∫ e^t * dt = (1/6)*e^t + C = (1/6) * e^(3x^2) + C.

Espero haberte ayudado.

Por favor, vuelve a enviar la imagen para que podamos ayudarte.