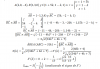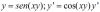Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Heide Solorzano
el 19/10/16

Heyyy, hola chic@s me podrían ayudar por favor, tengo estas demostraciones, se cuales son verdaderas y falsas pero no se como demostrarlas analíticamente, ya tengo algunas, porfas ayúdenme, mi fuerte no es la teoria...
••0 voto/s
•
Ángel
el 19/10/16
¿Qué demostraciones?

Un saludo

•0 voto/s
•

Cancelar
Matias Diaz Cid
el 19/10/16

Hola, me gustaría saber cuando es recomendable usar método de los discos en vez de capas cilíndricas y viceversa ,para calcular volúmenes. Gracias de antemano

••0 voto/s
•
Ángel
el 19/10/16
El método de discos y de capas cilíndricas se distinguen porque en el de discos el rectángulo representativo es siempre perpendicular al eje de giro, mientras que en el de capas es paralelo.

Un saludo

•0 voto/s
•

Cancelar
Sebastián
el 19/10/16

Hola, alguien me podría ayudar con este ejercicio???
Un triángulo tiene como vértices (2.0,-4) y (1,3,0), y el tercer vértice esta sobre la recta: (x,y,z) = k (5,-1,0) + (1,1,1). Hallar el tercer vértice para que el área del triángulo sea mínima.
Gracias!

••0 voto/s
•
Antonio Silvio Palmitano
el 19/10/16
Recuerda que la expresión del área de un triángulo con vértices A, B y C puede escribirse:
A = (1/2) * | BA x BC | (*), en la que BA y BC son vectores.
Tenemos dos vértices: A(2,0,-4) y B(1,3,0),
y podemos plantear el tercero, a partir de la ecuación vectorial de la recta a la que pertenece y queda: C(5k+1,-k+1,1).
Luego planteamos los vectores:
BA = < 2 - 1 , 0 - 3 , - 4 - 0 > = < 1 , - 3 , - 4 >
BC = < 5k+ 1 - 1 , - k + 1 - 3 , 1 - 0 > = < 5k , - k - 2 , 1 >
Luego planteamos su producto vectorial (cruz) y queda:
BA x BC = < - 4k - 5 , 20k + 1 , -16k - 2 >.
Luego, planteamos la expresión de su módulo elevado al cuadrado:
|BA xBC|^2 = (- 4k - 5)^2 + (20k + 1)^2 + (-16k - 2)^2 = desarrollamos:
= 16k^2 - 40k + 25 + 400k^2 + 40k + 1 + 256k^2 + 64k + 4 = reducimos términos semejantes:
= 672k^2 + 64k + 30, por lo que tenemos que el módulo del producto vectorial queda:
|BA x BC| = V(672k^2 + 64k + 30), observa que es una expresión en función de una variable k, luego sustituimos en la expresión del área señalada (*) y obtenemos la expresión del área del triángulo en función de la variable k:
A(k) = (1/2)*V(672k^2 + 64k + 30).
Luego solo queda que hagas el estudio de función para encontrar extremos, como seguramente has hecho en clase.
Espero haberte ayudado.

•1 voto/s
•
Antonius Benedictus
el 19/10/16
Es esto, Lucas:

•1 voto/s
•

Cancelar
miky
el 19/10/16

Por fa Amigos me ayudarían o me explicarían como podrían hacer estos ejercicios es que no los entiendo.

••0 voto/s
•
Matías Ignacio Loyola Galdames
el 19/10/16
Pero qué hay que hacer? Si puedes poner el enunciado por favor.

•0 voto/s
•
miky
el 19/10/16
Factorizacion

•0 voto/s
•
Matías Ignacio Loyola Galdames
el 19/10/16
Aquí tienes algunos. Ojalá puedas seguir.

•0 voto/s
•
miky
el 19/10/16
Muchas gracias ya me diste una pauta.

•1 voto/s
•

Cancelar
Otman Zeddam
el 18/10/16

HAY ALGUN UNICOO QUE ESTUDIA EL GRADO DE ADE ?
••0 voto/s
•
David
el 19/10/16
¿Por?

•0 voto/s
•
Otman Zeddam
el 19/10/16
pues que acabo de entrar a este grado este año y voy jodido con las mates..

•0 voto/s
•

Cancelar
alf lau
el 18/10/16

hola unicos   tengo una duda :
En caso que tenga alguno de estos elementos: determina si tiene máximos, mínimos y/o puntos de inflexión horizontales (atención, sólo los horizontales) $f left parenthesis x right parenthesis equals fraction numerator negative 3 over denominator x squared minus 9 end fraction$ Dada la función
En caso de que no lo tenga, expon el procedimiento a partir del cuál llegas a esta conclusión.
- calcula el valor de la función en ese valor de x para determinar el punto.
- justifica si se trata de un máximo o mínimo local y/o un punto de inflexión y
- desarrolla el proceso para determinar en qué valor de x la función lo alcanza,

la derivada me da      6x / x^4 -18x^2+81   e igualando a cero   x=0.
los siguientes puntos no me aclaro   ya que veo que no tiene maximos y minimos.

••1 voto/s
•
Antonio Silvio Palmitano
el 18/10/16
Observa que la derivada primera se anula para x=0, por lo que es un posible maximo o minimo.
Debes volver a derivar, para luego investigar la existencia de posibles inflexiones. Si haces todo, la derivada segunda queda:
- 18(x^2 + 3)/(x^2 - 9)^3.
Observa que nunca se anula en el dominio de la funcion, por lo que su grafica no presenta inflexiones.
Observa que para x=0 la derivada segunda toma un valor positivo, por lo que tenemos concavidad hacia arriba, y tenemos un minimo para x=0.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Juli Ramos Monge
el 18/10/16

••0 voto/s
•
Antonius Benedictus
el 18/10/16
Como la función es continua y se define igual por la izquierda que por la derecha, coincide exactamente con f(x)=4-x^2
Por tanto, como f'(x)=-2x, se tendrá que f'(1)=-2

•1 voto/s
•

Cancelar
Jordi García
el 18/10/16

Aquí va otra pregunta para que no os aburráis:

¿Cuántas veces puede restarse el número 1 del número 1.111?

PD: si no te doy 5 estrellas significa que no la has acertado :D

••0 voto/s
•
Matías Ignacio Loyola Galdames
el 18/10/16
jaja está buena.
Según yo, Infinitas, le puedes restar todo lo que quieras y vas a llegar hasta el infinito negativo.

•0 voto/s
•
Matias Diaz Cid
el 19/10/16
jaja yo creo que es una vez porque después de esa pasaría a hacer el numero 1.110

•0 voto/s
•
Matías Ignacio Loyola Galdames
el 19/10/16
Ahora me acordé, si había visto eso jaja.
Pero si ponemos 1.111 - 1 x n veces
ok no...

•0 voto/s
•

Cancelar
Andrea Diosdado
el 18/10/16

Hola!!!! Me piden un ejercicio de a partir del log₁₀2 = 0'3010 calcular los siguientes log..
a.16 b.0'25 c.0'625 d.250
Muchas gracias!!!!

••0 voto/s
•
Axel Morales Piñón.
el 18/10/16
Enunciado original Andrea(-:

•1 voto/s
•
César
el 18/10/16
creo que faltaria el dato del log(5)

•1 voto/s
•
Antonius Benedictus
el 18/10/16
log(5)=log(10/2)=log(10)-log(2)=1-log(2)=0'699
Y ya puedes.

•1 voto/s
•

Cancelar
Miquel Martos Doroteo
el 18/10/16

Estoy empezando a realizar derivadas implicitas y he intentado hacer éste ejrcicio, pero no consigo sacarla. ¿Me podrían ayudar por favor? La ecuación es: y = sen(xy);
Les ajdunto lo que he intentado hacer.

••0 voto/s
•
Matías Ignacio Loyola Galdames
el 18/10/16
Ojalá te sirva.

•1 voto/s
•
Antonius Benedictus
el 18/10/16
Atento a la regla de la cadena, Miquel:

•0 voto/s
•
César
el 18/10/16
Va Miquel ten en cuanta que y es funcion de x y(x)

•1 voto/s
•

Cancelar