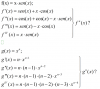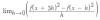-
Hola unicoos,,
Me cuestan mucho los problemas y en este no entiendo muy bien lo que quieren decir los porcentajes y lo que habría que hacer:
Un inversor, que tiene 28000€, coloca parte de su capital en un banco al 8% y el resto en otro banco al 6%. Si la primera parte le produce anualmente 200€ más que la segunda, ¿Cuánto colocó en cada banco?
Me podrían ayudar? Muchisimas gracias.
-
Factoriza y resuelve:
x^3+ 6x^2 – 7x – 60 = 0
Sabeís como se hace? Puedo hacerlo sin hacer el Ruffini? He intentado factorizarlo así:
60x (x+7)(x–1) = 0
El resultado factorizado es (x+5)(x+4)(x–3)

Matías Ignacio Loyola Galdames
el 18/10/16Si el grado de la x de mayor grado es mayor a 2, te conviene hacerlo con los divisores. Divides los divisores del término libre por los de la x de mayor grado y esos son los posibles raíces racionales.
En este caso el término libre es -60 y el de la x de mayor grado es 1
Entonces divisores de -60: 1,2,3,4,5.... etc (también con negativos)
divisores de la x de mayor grado: 1,-1
Entonces los posibles son: 1/1, 2/1, 3/1.... etc. (también negativos)
Y ahí vas probando con qué números te da 0. En este caso con -5, -4, 3 (obviamente máximo son 3)
Como el grado mayor es 3, si sacas una raíz. Por ej tres. Entonces (x-3) es factor. Divides el polinomio por (x-3) y te queda uno de segundo grado que es más fácil de calcular sus raíces.
No sé si fui claro, ojalá entiendas.
-
Me han puesto este ejercicio de gaus y no dimos nada en clase :( no se como hacer la ecuacion, me lio...
Ejercicio 2
Tres amigos compran acciones de tres valores: la empresa aseguradora ABX (A), el Banco BETRIX (B) y la empresa de construcciones CONSUR (C).
Calcula cuánto vale cada una de las acciones si:
•Félix ha comprado 100 acciones de A, 60 de B y 20 de C, y ha tenido que pagar 1.660€
.
•Damián ha comprado 60 acciones de A, 10 de B y 100 de C, y ha desembolsado 1.570 €
.
•Carlos, que ha gastado 1.560 €, tiene 30 acciones de A y 150 de C
Resolver por el método de Gauss, sistema escalonado
-
-


Antonio Silvio Palmitano
el 18/10/16Recuerda lo órdenes de magnitud: cuando w tiende a +infinito tenemos que lnw << w^p << b^w, con p > 0 y b > 1.
1) Comencemos con la expresión de la función:
f(x) = 2^x - x^2 = 2^x * ( 1 - x^2 / 2^x )
luego, al tomar el límite cuando x tiende a +infinito, aplicamos la propiedad del límite de un producto de funciones y queda:
Lím(x-->+inf) f(x) = Lím(x-->+inf)(2^x) * Lím(x-->+inf)( 1 - x^2 / 2^x ) = +inf,
observa que el primer factor (exponencial con base mayor que 1) tiende a +infinito, y que el segundo factor tiende a 1 (su primer término es constante, y el segundo tiende a cero por órdenes de magnitud).
2) Observa que el argumento del logaritmo es una expresión fraccionaria (llamamos N a su numerador, y D a su denominador).
Veamos el numerador: observa que el argumento del logaritmo es un binomio de grado dos, por lo tanto extraemos factor común x^2 y queda:
N = ln( x^2 * (1 + 1 / x^2 ) ) = aplicamos propiedades de los logaritmos = 2lnx + ln( 1 + 1 / x^2 ).
Luego, vamos a la expresión de la función (observa que D = x), distribuimos el denominador y queda:
f(x) = 2lnx/x + ( ln( 1 + 1 / x^2 ) ) / x.
Luego pasamos al límite, aplicamos la propiedad del límite de una suma de funciones y queda:
Lím(x-->+inf) f(x) = Lím(x-->+inf)( 2 lnx / x ) + Lím(x-->+inf)( ( ln( 1 + 1 / x^2 ) ) / x ) = 0 + 0 = 0,
observa que el primer término tiende a cero por órdenes de magnitud, y que en el segundo término el numerador tiende a cero y el denominador tiende a infinito).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/10/16(a) Es Falsa, y puedes proponer un contraejemplo: f(x) = 1, g(x) = 2x, h(x) = x^2, luego planteamos ambos miembros de la igualdad por separado:
(h o (f+g))(x) = definición de composición = h( (f+g) )(x) = definición de suma de funciones = h( f(x) + g(x) ) = h(1 + 2x) = (1 + 2x)^2 = 1 + 4x + 4x^2;
( (hof) + (hog) )(x) = definición de suma de funciones = (hof)(x) + (hog)(x) = definición de composición = h( f(x) ) + h( g(x) ) = h(1) + h(2x) = 1^2 + (2x)^2 = 1 + 4x^2;
como los desarrollos nos conducen a expresiones distintas, concluimos que la proposición es falsa.
(b) Es Verdadera, por lo que desarrollamos ambos miembros de la igualdad en forma general:
( (f*g) o h )(x) = definición de composición = (fg)( h(x) ) = definición de función producto = f( h(x) ) * g( h(x) )
( (foh)*(goh) )(x) = definición de función producto = (foh)(x) * (goh)(x) = definición de composición = f( h(x) ) * g( h(x) )
como los desarrollos generales nos conducen a la misma expresión general, concluimos que la proposición es verdadera.
(c) Es Verdadera, por lo que desarrollamos ambos miembros de la igualdad en forma general:
( (f+g) o h )(x) = definición de composición = (f+g)( h(x) ) = definición de función suma de funciones = f( h(x) ) + g( h(x) )
( (f o h) + (g o h) )(x) = definición de función suma = (f o h)(x) + (g o h)(x) = definición de composición = f( h(x) ) + g( h(x) )
comos los desarrollos generales nos conducen a la misma expresión general, concluimos que la proposición de verdadera.
(d) Es Falsa, por lo que puedes proponer un contraejemplo: f(x) = 3, g(x) = 2x, h(x) = x^2, luego planteamos ambos miembros de la igualdad por separado:
( h*(f o g) )(x) = definición de función producto de funciones = h(x) * (f o g)(x) = definición de composición = h(x) * f( g(x) ) = sustituimos expresiones:
= x^2 * f(2x) = sustituimos expresión = x^2 * 3 = 3x^2;
( (h*f) o g )(x) = definición de composición = (h*f)( g(x) ) = definición de función producto de funciones = h( g(x) ) * f( g(x) ) = sustituimos expresiones:
= h(2x) * f(2x) = sustituimos expresiones = (2x)^2 * 3 = 4x^2 * 3 = 12x^2;
como los desarrollos nos conducen a expresiones distintas, concluimos que la proposición es falsa.
Espero haberte ayudado.