-
¿Podrían ayudarme con este ejercicio de selectividad por favor? Tan solo quiero saber el apartado a) ya que no se como empezar. Muchísimas gracias.

César
el 30/8/16Tenemos un vector de la recta y un punto A exterior a ella. Podemos saber cualquier pùnto generico de la recta.
La recta en forma parametrica es
x=1+λ
y=1-2λ el vector direcciopn es v=(1,-2,1)
z=1+λ un vector que una el punto A con un punto genérico de la recta es (2-(1+λ),2-(1-2λ),2-(1+λ))=u=(1-λ),(1+2λ),(1-λ)
si hacemos u.v=0 ambos vectores serán perpendiculares
(1,-2,1).((1-λ),(1+2λ),(1-λ))=0 => λ=0 Luego el punto que cumple ese criterio es P=(1,1,1) siendo el vector de direccion de la recta pedida que en forma vectorial será
(x,y,z)=(2,2,2)+t(1,1,1)
-
¿Podrian resolverme este problema? O decidme en que video aparece? gracias.
La temperatura en Cº de un refresco "t" horas despues de ser introducido en un frigorifico, viene dada por:
T(t)=30t^2+15/8t^2+2t+1. Halla:
a) La temperatura inicial del refresco y despues de 3 horas.
b) La temperatura que alcanzara el refresco a lo largo del tiempo.
Gabriel
el 30/8/16En primer lugar, me parecería extraño que el primer sumando para el cálculo de la temperatura sea t^2 y no t^3, puesto que es un polinomio y parece que el exponente del tiempo debería de ir disminuyendo, es decir, ser algo del tipo...
T(t)=30t^3+15/8t^2+2t+1
En segundo lugar, vayamos con el problema.
El primer apartado al ser la fórmula para la temperatura en ºC, y el tiempo en horas, no tendrías más que sustituir el la "t" por "3", así daría 293,875 ºC o 833,875 ºC según si utilizaras tu fórmula o la mía
El segundo apartado tendrías que calcular la derivada de la temperatura para calcular cómo varía a lo largo del tiempo.
Tu fórmula, T(t)'=2·30t+2·15/8t+2
Mi fórmula, T(t)'=3·30t^2+2·15/8t+2
Espero haber sido útil.
Saludos. -
Hola. En el siguiente problema la solución no me convence, ¿Podríais ayudarme? Gracias.
Un lado de un rombo está sobre la recta 3x+y-5=0 , sabiendo que los vértices opuestos del rombo son los puntos (1,2) y (4,9), calcula los otros vértices. -
Hola,en resta de fracciones solo se pueden retirar todos los denominadores cuando se trate de una ecuacion. y que no se puede hacer si es una funcion o una expresion algebraica.
adjunto foto de una ecuacion en la que el comun denominador no se hace a todos los terminos de la ecuacion y no entiendo porque., si es una Ecuacion.
lo que ocurre es que no se diferenciarlas. me poneis por favor un ejemplo resuelto de resta de cada una de las tres- ecuacion, funcion, expresion algebraica.
gracias -
hola
me podeis ayudar si esta bien este ejercicio es que lo he intentado de todas formas y no me sale, gracias un saludo -
Hola! Me explicáis tambn como calcular una cosa de límites porfaa? En este ejercicio se como calcular con x=3 que seria con los laterales, pero...y con el 2?? Gracias!

Gabriel
el 30/8/16Es sencillo, para calcular en x=2, tienes que coger el trozo de la función para x<3, puesto que 2<3. Así te daría el límite con valor 7/3.
Para x=3, a menos que se haya confundido, NO PODRÍAS CALCULAR SU LÍMITE, NO EXISTE. El caso es que te define la fución para cuando es x<3 y x>3, no para x=3, por lo que al no existir la función, no existe el límite.
Saludos. -
Hola! Me podéis ayudar con este límite porfa!! Lo he repetido racionalizando muchas veces y me da 0 mientras q la solución es -1/56. Gracias!


Antonio Silvio Palmitano
el 30/8/16Observa que si calculamos los límites por separado, tanto el numerador como el denominador tienden a cero, por lo tanto el límite es indeterminado.
Luego, para salvar la indeterminación, operaremos multiplicando al numerador (N) y al denominador (D) por la expresión "conjugada" del numerador, que es el que presenta una expresión irracional.
También observa que el denominador es una diferencia de cuadrados, por lo que es factorizable.
Comencemos:
N = ( 2 - V(x - 3) )( 2 + V(x - 3) ) = 4 - ( V(x - 3) )^2 = 4 - (x - 3) = 7 - x = - (-7 + x) = -1(x - 7).
D = (x^2 - 49)( 2 + V(x - 3) ) = (x - 7)(x + 7)( 2 + V(x - 3) )
Luego observa que las expresiones N y D comparten el factor (x - 7), lo simplicamos y queda:
Lím(x--> 7) N/D = Lím(x--> 7) (-1) / ( (x + 7)( 2 + V(x - 3) ) = -1 /(14*4) = -1/56.
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 30/8/16Tienes la ecuación trigonométrica (indicamos alfa con A):
senA = sen(2A)
luego, por identidad trigonométrica del seno del duplo de un ángulo queda:
senA = 2*senA*cosA
haces pasaje de término y queda:
senA - 2*senA*cosA = 0
extraes factor común a la izquierda y queda:
senA * (1 - 2*senA ) = 0
luego, por tratarse de un producto igualado a cero, tenemos dos opciones:
1)
senA = 0
luego componemos con la función inversa del seno y queda:
A = arcsen0, resolvemos y llegamos a:
A = 0, o 180°, o 360°, o 540°, o ... , que podemos expresar en general:
A = 180° * k, con k perteneciente al conjunto de los números enteros.
2)
1 - 2*senA = 0, depejamos y queda:
senA = 1/2 (observa que hay ángulos en el primero y en el segundo cuadrante cuyo seno es positivo)
luego componemos con la función inversa del seno y queda:
A = arcsen(1/2), que nos conduce a dos opciones:
2a)
A = 30°, o 390°, o 790°, o ..., que en general pueden expresarse:
A = 30° + 360° * m, con m perteneciente al conjunto de los números enteros;
2b)
A = 150°, o 510°, o 870°, o ... , que en general pueden expresarse:
A = 150° + 360° * n, con n perteneciente al conjunto de los números enteros.
Observa que las soluciones para esta ecuación son: 0°, 30°, 150°, 180° si nos restringimos al intervalo: [0°,360°).
Espero haberte ayudado. -
Me pueden ayudar con este problema:
Hallar la ecuación de la parábola de eje paralelo al eje Y y que pasa por los puntos (-6,3),(-4,5),(-1,0).
Lo que hice fue reemplazarlo en su respectiva ecuación general P: Ax²+Dx+Ey+F pero tengo dificultades resolviendo el sistema.







_Thumb.jpg)
_Thumb.jpg)








_Thumb.png)




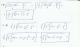


_Thumb.jpg)
