-


Antonio Silvio Palmitano
el 15/8/16Has comenzado muy bien. Observa la ecuación que ha quedado luego de sustituir y = xu, luego de operar te quedó:
xu ' = - e^u
escribimos u ' como cociente de diferenciales y queda:
xdu/dx = - e^u
hacemos pasajes de factores buscando separar variables y queda:
du/(-e^u) = dx/x (observa bien aquí)
observa que en el miembro de la izquierda, por propiedades de las potencias podemos escribir:
- e^(-u) du = (1/x) dx
luego integramos y queda:
e^(-u) = ln|x| + C
Observa que has llegado a la solución correcta, pero te faltó un signo en el exponente de la exponencial.
Espero haberte ayudado.
-
Hola alguien puede ayudarme con alguno de estos ejercicios, para que me sirva de ejemplo, por favor.
2) Se lanzan dos dados en un juego en el que participan dos jugadores. El primero gana cuando
la suma de las puntuaciones es impar. El segundo, cuando la suma es par y múltiplo de 3. Halla
la probabilidad de que gane: a) el primero;b) el segundo; c) ninguno de ellos.
3) En la consulta de un médico hay 10 pacientes: 5 tienen gripe; 3, problemas digestivos, y 2,
alergia. Si se eligen 3 enfermos al azar, halla la probabilidad de que: a) los tres tengan
enfermedades distintas; b) los tres tengan la misma enfermedad.
4) La probabilidad de que un jugador de tenis gane un partido es de 0,25. Si juega cuatro
partidos, calcula la probabilidad de que gane: a) exactamente dos partidos; b) por lo menos dos
partidos.
5) Para medir el peso de los peces de una piscifactoría, se utiliza una variable aleatoria normal
cuya media es de 220 Kg y su desviación típica es de 20 Kg. Calcula la probabilidad de obtener
un pez que tenga un peso: a) superior a 200 Kg; b) entre 180 y 250 Kg. -
alguien me ayuda a probar esto:
y de paso me tira algun tip o algo como encarar cuando te piden demostraciones y pruebas. (en general)
En este caso es de numero complejo: |Z1+Z2|≤|Z1|+|Z2|
(1 Y 2, son subindices)

Antonio Silvio Palmitano
el 15/8/16Para demostrar, debes tener en cuenta varias propiedades de los números complejos, de sus conjugados y de sus módulos.
Presta atención al paso en que introducimos la desigualdad, allí se aplica la propiedad: "el conjugado del conjugado de un número complejo es igual al número complejo".
Envío una foto con un esquema de la demostración.
Espero haberte ayudado.Envío una foto con un esquema de la demostración.
Espero haberte ayudado.">
-
alguien me ayuda apasar este complejo a notacion BINOMICA. gracias
No comprendo como se hace e interpretar los valores que me dan
saludos

Antonio Silvio Palmitano
el 15/8/16Debes tener en cuenta las diferentes formas de escribir un número complejo:
Cartesianas (donde x es la parte real, y es la parte imaginaria):
Par ordenado: z = (x,y)
Binómica: z = x + yi
Forma Polar: z = |z|t (donce |z| indica módulo del número complejo, t (theta) indica argumento del número complejo, con 0 <= t < 2pi)
Forma Trigonométrica: z = |z|(cost + isent)
Forma Exponencial: z = |z|e^it
(observa que las tres últimas fórmulas emplean módulo y argumento).
Ahora en tu ejercicio, obsrva que los segundos términos del numerador y del denominador están escritos en forma exponencial:
e^(pi/2)i = 1e^(pi/2)i = 1(cos(pi/2) + isen(pi/2)) = 1(cos(pi/2) + isen(pi/2)) = 1(0 + 1i) = 0 +1i = i (observa que hemos pasado de forma exponencial a forma trigonométrica,, y luego a forma binómica).
Por lo tanto, se trata de resolver:
(1 - i)/(1 + i) = (multiplicamos por el conjugado del denominador, tanto al numerador como el denominador y queda:)
= (1 - i)(1 - i))/((1 + i)(1 - i)) = (resolvemos por separado numerador y denominador y queda:)
= -2i/2 = -i = (observa, a partir de un gráfico cartesiano, que el módulo es igual a 1, y el argumento es igual a 3pi/2)
= |1|(3pi/2).
Espero haberte ayudado. -
hola disculpen este ejercicio no me sale me pueden ayudar:
Hallar la ecuación de la circunferencia tangente a las circunferencias x² + y² -3x -6y +10 = 0 y x² +y² = 5 en su punto común y además es tangente a la recta x -2y -1=0 -
Hola unicoos!!
Quisiera saber si alguien pudiese ayudarme con estos ejercicios... De integrales. Busque en videos pero no encontre nada parecido... Solo integrales trigonometricas.
Se que en A . debo usar el cambio de variable en ln... Pero mi resultado no llega al resultado dado por el profesor y no se que hacer ( 2x^(1/2)) (lnx-2^1/2)
Y en el ejercicio B se que es por partes pero al igual que el anterior no ae como aplicar la teoria. -
Me pueden ayudar con esta ecuación la hice como 6 veces y las bases no me deja igualarlas cuando vuelvo a pasar variable, incluso expresando el resultado en logaritmo
3^x + 1/(3^x+1) = 28/9
Al cambiar variable me queda esta ecuación 3t^2+28t+3= 0






_Thumb.png)

_Thumb.jpg)



_Thumb.jpg)
_Thumb.png)


_Thumb.jpg)
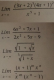

_Thumb.png)

_Thumb.png)






_Thumb.png)



_Thumb.png)



_Thumb.png)


_Thumb.jpg)

_Thumb.jpg)


_Thumb.jpg)

_Thumb.jpg)
_Thumb.jpg)

_Thumb.jpg)

