-
-
¿Tengo una duda sobre límites?
El primer vídeo de treinta de límites que grava David en el minuto 9:38 que desarrolla el ejercicio cuatro, explica que al encontrarnos con una indeterminación de tipo ∞/∞ dividimos a todos lo términos entre las X de mayor grado, utilizando en ese caso la X del numerador.
En el vídeo cuatro de treinta en el minuto 1:25 explica que cuando se presenta la misma indeterminación se divide a todos los términos por la X de mayor grado del denominador.
Quiero saber si es un error en alguna de las dos explicación y cual sería la correcta; o es algún paso de límites que no estoy entendiendo.
Muchas gracias. -


Antonio Silvio Palmitano
el 12/8/16Tenemos la ecuación:
16 * 5^(2x) = 25 * 20^x
Observa que se pueden factorizar: 16 = 2^4, 25 = 5^2, 20 = 2^2 * 5
reemplazamos y queda:
2^4 * 5^(2x) = 5^2 * (2^2 * 5)^2
distribuimos en el segundo factor de la derecha y queda:
2^4 * 5^(2x) = 5^2 * 2^4 * 5^2
luego cancelamos el factor 2^4 en ambos miembros, resolvemos producto de potencias con bases iguales a la derecha y queda:
5^(2x) = 5^4
luego, vemos que las bases coinciden, por lo tanto los exponentes son iguales:
2x = 4
despejamos y llegamos a:
x = 2.
Es conveniente reemplazar en la ecuación inicial y verificar la validez de la solución a la que hemos llegado.
Otro camino para resolver sería aplicar logaritmos.
Espero haberte ayudado.

Antonio Silvio Palmitano
el 12/8/16Tiene razón, gracias Colega, se me han deslizado errores. Reparamos (los profesores también nos equvocamos, y bastante seguido):
Tenemos la ecuación:
16 * 5^(2x) = 25 * 20^x
observa que podemos expresar al segundo factor de la izquierda como potencias sucesivas y queda:
16 * (5^2)^x = 25 * 20^x
luego resolvemos la base en el segundo factor de la izquierda y queda:
16 * 25^x = 25 * 20^x
luego hacemos pasajes de factores como divisores y queda:
25^x / 20^x = 25 / 16
luego asociamos bases a la izquierda y queda:
(25/20)^x = 25/16
luego simplificamos la base a la izquierda y queda:
(5/4)^x = 25/16
luego, observa que tenemos un cuadrado a la derecha, lo expresamos y queda:
(5/4)^x = (5/4)^2
y ahora si, por comparación, llegamos a la solución:
x = 2.
Gracias Colega Peter nuevamente, disculpen Alexis y Unicoos por el error involuntario cometido anteriormente.
Ahora sí, espero haberte ayudado.
Es conveniente reemplazar en la ecuación inicial y verificar la validez de la solución a la que hemos llegado.
Otro camino para resolver sería aplicar logaritmos.
Espero haberte ayudado. -
Buenas noches, tengo una duda sobre la diagonalización de matrices. A la hora de determinar si una matriz es diagonalizable afecta en algo que las raíces del polinomio característico hayan salido dobles o triples o solo por no ser raíces complejas ya puedo afirmar que esa matriz es diagonalizable?
-
una cometa a 100 pies sobre el suelo se mueve horizontalmente con una velocidad de 8 pies/s ¿con que velocidad cambia el angulo formado por el hilo y la horizontal, cuando se ha soltado 200 pies de hilo?
Alguien me ayuda he tratado de hacerlo pero creo que esta malo :/

Antonio Silvio Palmitano
el 12/8/16Te envío una foto, con un esquema hecho a mano.
Hemos designado como x al nivel del suelo. Hemos designado a y como eje de alturas, y hemos señalado un punto en el primer cuadrante indicando la posición de la cometa.
Observa que nos ha quedado determinado un triángulo rectángulo.
Luego, todo se trata de plantear relaciones trigonométricas, y de derivar con respecto a la variable t (tiempo). A este respecto, ten en cuenta que x es la posición horizontal de la cometa, y que su derivada con respecto al tiempo es la velocidad horizontal de la misma, que es un dato del enunciado.
Espero haberte ayudado. -
unicoos perdonen si estoy molestando mucho, pero me ayudarian con esta otra demostracion, es que no entiendo como puedo demostra algo que es tan simple. se trata de la transpocision de la matriz identidad. Ayudenme por favor. Y si pudieran indicarme un pdf donde se encuentren algunas demostraciones y expliquen con claridad las operaciones, seria genial.






_Thumb.jpg)



_Thumb.jpg)

_Thumb.png)

_Thumb.png)

_Thumb.jpg)


_Thumb.jpg)


_Thumb.jpg)












_Thumb.png)

_Thumb.png)

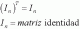

_Thumb.jpg)


_Thumb.jpg)

