-
Buenas a todos
Estoy resolviendo un problema pero me parece que estoy yendo por mal camino:
"Un campo tiene 250 árboles con olivos y almendros. Si el doble de almendros son 10 menos que todos los olivos, ¿cuántos almendros/olivos hay?"
Por ahora lo he planteado de la siguiente forma:
Olivos=X /// Almendros=Y
2x = y−10
2x−y = -10
Pensé que se podía mediante un sistema de ecuaciones (por que hay X e Y) pero para eso harían falta dos ecuaciones, ¿no?
¿Cómo debería resolver este problema?
Por ahora lo he planteado de la siguiente forma:
Olivos=X /// Almendros=Y
2x = y−10
2x−y = -10
Pensé que se podía mediante un sistema de ecuaciones (por que hay X e Y) pero para eso harían falta dos ecuaciones, ¿no?
¿Cómo debería resolver este problema?">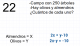


Antonio Silvio Palmitano
el 8/7/16Observa bien: x + y = 250 expresa la cantidad total de árboles.
Pero observa también que "el doble de almendros" queda expresado por el término 2y,
y la segunda ecuación queda: 2y = x - 10, que corresponde a "el doble de almendros son 10 menos que todos los olivos".
Por lo tanto, el sistema de ecuaciones a resolver queda:
x + y = 250
2y = x - 10
Puedes resolverlo, y verás que su solución es:
x = 170 olivos
y = 80 almendros.
Espero haberte ayudado.
-
Hola me gustaria saber como desarrollar un binomio para hacerlo cuadrado perfecto.
Esto es para obtener la formula para poder representar la circunferencia/elipse, etc..
Teniendo 4x^2+2x - 4y^2 -3y -10 = 0
Cuales serian los pasos para obtener el cuadrado perfecto de ambos binomios?.

Antonio Silvio Palmitano
el 8/7/16Primero comienza por extraer como factor común los coeficientes de los términos cuadráticos para cada incógnita, y hacer pasaje de término independiente, verás que la ecuación queda:
4*(x^2 + (1/2)*x) - 4*(y^2 + (3/4)*y) = 10
Luego, dentro de cada agrupamiento agregas un término igual "al cuadrado de la mitad del coeficiente del término lineal", que debes compensar a la derecha de la igualdad agregándolo, pero multiplicado por su factor común, lo haces y la ecuación queda:
4*(x^2 + (1/2)*x + (1/4)^2) - 4*(y^2 + (3/4)*y + (3/8)^2) = 10 + 4*(1/4)^2 - 4*(3/8)^2
Ahora si, verás que los dos agrupamientos corresponden a binomios elevados al cuadrado, resuelves a la derecha de la igualdad, y la ecuación queda:
4*(x + 1/4)^2 - 4*(y + 3/8)^2 = 155/16
Luego, como los coeficientes de los dos términos de la izquierda tienen valor absoluto 4, puedes dividir en todos los términos por 4 y la ecuación queda:
(x + 1/4)^2 - (y + 3/8)^2 = 155/16
Por último, divides en todos los términos por 161/64 y llegas a la ecuación canónica:
((x + 1/4)^2)/(155/16) - ((y + 3/8)^2)/(155/16) = 1
Como verás, se trata de una hipérbola equilátera con eje real paralelo al eje x, con centro de simetría C(-1/4,-3/8), semieje real a = V(155/16), semieje imaginario b = V(155/16), semieje focal c = V(155/16 + 155/16) = V(155/8), y solo te resta expresar las ecuaciones de las asíntotas: y = x - 1/8, e y = -x - 5/8.
Espero haberte ayudado. -
Buenas!!
Quería pedirle, si podría pasarme ejercicios de repaso, o algún lugar para encontrarlos, es que me ha caído matemáticas para septiembre y necesito repasar y mucho, los vídeos me ayudan mucho!!
Kevin
el 8/7/16Coincido con Mario; sería mejor si especificaras lo que necesitas.
De todas maneras, dejo aquí unos ejercicios de repaso que me han dado para el verano. Son de 3ro de ESO
Ejercicios de repaso:
http://www.edu.xunta.gal/centros/iesramoncabanillas/aulavirtual/file.php/142/Boletin_de_repaso_para_verano_3_o_ES1.pdf
Otros ejercicios de 3ro ESO:
http://www.edu.xunta.gal/centros/iesramoncabanillas/aulavirtual/course/view.php?id=142
Si te pide autorización, pulsa "Entrar como convidado" y listo. Aunque esa parte esté en gallego, todo está en español.
Saludos
Kevin -


Francisco Gutiérrez Mora
el 8/7/16A ver Jaume, lo que haces en el último paso no se puede hacer. ¿Cómo vas a dividir el radicando también por dos?
Es: (10±√88)/6=(10±√(4·22))/6=(10±2√22)/6 (Ahora sí puedes simplificar por dos y tenemos):(5±√22)/3 Si desdoblas la solución tenemos: x1=(5+√22)/3,; x2=(5-√22)/3
Espero que te ayude un saludo.

Francisco Gutiérrez Mora
el 8/7/16Jaume, intento aclararte un poco mejor tu error:
(10±√88)/2=(5±(√88)/2)/3. Aquí puedes entrar el 2 en la raíz, que como sabes entra elevado al cuadrado y sale con la raiz cuadrada extraída ¿vale? Pues bien nos queda:(5±√(88/4))3=(5±√22)/3
Como ves llegamos a la misma solución. Un Saludo, amigo.

Francisco Gutiérrez Mora
el 8/7/16Sí, Jaume: √88=√4·22 el cuatro lo puedes sacar de la raiz, puesto que está multiplicando, y te queda 2√22. Espero que lo entiendas. Esto lo hacemos para dar el resultado lo más simplificado posible. Valora las respuestas por favor, pues con ello veo lo que te han servido. Un Saludo

JAUME
el 8/7/16Jajaja. No no Francisco, estoy enfrascado con la recuperación de mates de 3º y 4º de mi hijo para que pueda pasar a 1º Bachillerato. Como ves mi nivel es pésimo no, lo siguiente. Voy a repasar detenidamente tu explicación para poder explicárselo a él. No me queda nada....
De nuevo darte las gracias por tu tiempo y por tu ayuda Francisco.
Un saludo. -
Que tal, buenos días. Otra de 2º grado. No me coincide la solución pero por poco. Donde tengo el error ? La solución debería ser 5+-raiz cuadrada de 22 dividido entre 3. Me falla la raíz cuadrada. He repasado pero no logro ver el error.
-
Holas unicoos, en este ejercicio tengo una duda, no se si la solución es 24 o -24. Tengo la duda de si la segunda columna la multiplico por -1 y la pongo en positivo o si saco el -2 directamaente. Gracias.
-


David
el 7/7/16De las tres primeras ecuaciones obten x,y,z... Sistema de ecuaciones con 4 incognitas Reduccion GAUSS o Sistema de ecuaciones - Metodo de CRAMER
Una vez tengas las tres medidas... Volumen y Superficie de un ORTOEDRO -
hola necesito ayudaaaaa!!! con este tipo de ejercicios: sean A= 1 4 b= -2 4 c= -1 x
-1 8 -1 7 y z hallar x,y,z ,t sabiendo que A + tC=B no encontré ningún vídeo de este tipo, gracias, estoy viendo ecuaciones matriciales, he retomado mis estudios después de mucho tiempo, aprendí hacer las-operaciones básicas con matrices y a despejar incógnitas , pero no se por donde empezar con este ejercicio, no encontré ningún vídeo parecido, por favor me ayudas ???
Muchas gracias Maria Jose

David
el 7/7/16Simplemente opera.. A+t.C=B
(1 4) (-2t 4t) (-1 x)
(-1 8) +(-t 7)=(y z)....
(1-2t 4+4t) (-1 x)
(-1-t 15)=(y z)....
1-2t=-1
4+4t=x
-1-t=y
15=z...
Pasa todsas las incognitas a un lado y resuelve el sistema.. Sistema de ecuaciones con 4 incognitas Reduccion GAUSS o Sistema de ecuaciones - Metodo de CRAMER



_Thumb.jpg)











_Thumb.png)
