-
Hola tengo un ejercicio que no entiendo como llega a tal conclusión.
Tengo que si aunmentar Tcaliente o disminuir Tfria. Nose por llega a esa conclusión mediante derivas parciales.
Gracias -
Gracias por existir Unicoos.
Si me atienden, se trata de una integral definida y os puede resultar graciosa porque hay que trabajarla un pelín. Puedo decirles que no se trata de una impropia y la he trabajado varias veces sin buenos resultados. Soy estudiante de química por la UNED y ya por estas fechas no puedo colgar nada en el foro.
Integral [(dx)/(2-x^2)^1/2] {límites de 0 a 1} y su resultado es {pi/4}.
En mis intentos intentó forzar un arc sin, pero ya sea porque haga mal el cambio de variable {hago t^2= x^2/2; x=[(2)^1/2]t] y dx=(2^1/2)dt} ó a la hora de sustituir los nuevos límites tras el cambio de variable que me quedan 0 y 2^1/2. No consigo el resultado.
Me llamo Juan y les mando un abrazote desde Tenerife por todo lo que me han ayudado. Saludos!
-
Holaa, me pueden ayudar con este ejercicio? El problema se me presentó donde dice que el centro del rectángulo tiene que estar en el origen de coordenadas, los rectángulos tienen dos lados mas largos que los otros dos, por lo que no encuentro la manera de hacer que sea un rectángulo manteniendo el punto que me indica y el centro en el origen de coordenadas. Para mi es un cuadrado...


Antonio Silvio Palmitano
el 7/7/16Primero imagina el rectángulo con sus diagonales trazadas, llamamos centro al punto de intersección de las dos diagonales que, además, es el punto medio para ambas.
Por lo tanto, te han dado datos suficientes para trazar media diagonal, que es el segmento que une el origen (0,0) con el punto representativo del número complejo dato, que es a(3,3), luego extiendes el segmento guardando simetría con el origen, y obtienes el segundo punto que es c(-3,-3) (observa que el punto c representa al opuesto del complejo dato).
Luego, a partir del punto a trazas una recta paralela al eje y, y desde el punto c trazas una paralela al eje x, y verás que su punto de intersección es b(3,-3) (observa que el punto b representa al conjugado del complejo dato).
Luego, a partir del punto a trazas una recta paralela el eje x, y desde el punto c trazas una paralela al eje y, y verás que su punto de intersección es d(-3,3) (observa que el punto d representa al opuesto del conjudado del complejo dado.
Ya tienes los cuatro vértices y puedes continuar.
Espero haberte ayudado. -
Buenas noches.Alguien podria mostrarme como calcular el dominio de esta funcion? F(x)=log(4-x^2)
Gracias

Armando Fiorini
el 7/7/16Es sencillo, lo que esta dentro de log, tiene que ser positivo, entonces como 4-x^2 es una diferencia de cuadrados, lo factorizas, ves cuando se hace cero, pruebas valores en los intervalos, y donde te de positivo, ese sera el dominio, ojo, en -2 y 2 no se incluye porque es mayor estricto que 0, saludos!

Gabriel
el 7/7/16Es que estoy mareado con el ejercicio.Mira, tengo f(x)=raiz cuarada de x^2 -1 y tengo g(x)=raiz de 1-x
Tengo qe hacer f(g) osea armar la compuesa.Y el problema que tengo es en calcular el dominio de F(g).Porque necesito que me equede la condicion, osea si x es igual,mayor o menor que 0. Pero no me sale el dominio...




_Thumb.jpg)

_Thumb.jpg)








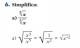

_Thumb.jpg)




_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)


_Thumb.jpg)


_Thumb.jpg)


_Thumb.png)

_Thumb.png)

