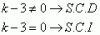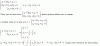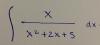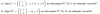-
 no estoy seguro,creo que el dato de que la recta que esta incluida En el plano es solucion del sistema es irrelevante,debo hacer Gauss y resolverlo?.
no estoy seguro,creo que el dato de que la recta que esta incluida En el plano es solucion del sistema es irrelevante,debo hacer Gauss y resolverlo?.

Antonio
el 19/1/20Al resolver el sistema se obtiene:
Si k ≠0,1,-1 el sistema es compatible determinado: los planos se cortan en un punto; no nos sirve.
Si k=0 el sistema es incompatible: los planos no se cortan; no nos sirve,
Si k=±1 el sistema es compatible indeterminado: los planos se cortan en una recta; nos sirve,
Si k=1 la recta no está en el plano dado, no nos sirve,Si k=-1 la recta está en el plano dado, por lo que:
la solución es: k=-1
-


Antonio Silvio Palmitano
el 19/1/20Tienes la ecuación polinómica cúbica:
x3 - 2x2 - x + 2 = 0,
extraes factor común (x2) en los dos primeros términos, extraes factor común (-1) en los dos últimos términos, y queda:
x2*(x - 2) - 1*(x - 2) = 0,
extraes factor común [(x - 2)], y queda:
(x - 2)*(x2 - 1) = 0,
factorizas el segundo agrupamiento (observa que tienes una resta de cuadrados perfectos), y queda:
(x - 2)*(x + 1)*(x - 1) = 0;
luego, por anulación de una multiplicación, tienes tres opciones:
1°)
x - 2 = 0, aquí sumas 2 en ambos miembros, y queda: x = 2,
2°)
x + 1 = 0, aquí restas 1 en ambos miembros, y queda: x = -1,
3°)
x - 1 = 0, aquí sumas 1 en ambos miembros, y queda: x = 1;
luego, con las tres soluciones que tienes remarcadas, tienes que el conjunto solución de la ecuación de tu enunciado queda expresado:
S = { -1 , 1 , 2 }.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/1/20Vamos con una orientación.
Observa que puedes operar en el denominador del argumento de la integral:
x2 + 2x + 5 = x2 + 2x + 1 - 1 + 5 = (x2 + 2x + 1) + (-1 + 5) = (x + 1)2 + 4;
luego, sustituyes esta expresión en el denominador del argumento de tu integral, y queda:
I = ∫ ( x/[(x + 1)2 + 4] )*dx (1).
Luego, puedes plantear la sustitución (cambio de variable:
x + 1 = w (1), de donde tienes:
dx = dw (2), y también tienes:
x = w - 1 (3);
luego, sustituyes las expresiones señaladas (1) (2) (3) en el argumento de la integral señalada (1), y queda:
I = ∫ ( (w - 1)/[w2 + 4] )*dw,
distribuyes el denominador en el argumento de esta integral, y queda:
I = ∫ ( w/[w2 + 4] - 1/[w2 + 4] )*dw,
aplicas la propiedad de la integral de una suma de funciones, yqueda:
I = ∫ ( w/[w2 + 4] )*dw - ∫ ( 1/[w2 + 4] )*dw,
y luego queda que resuelvas las dos integrales remarcadas (observa que en la primera puedes plantear la sustitución: p = w2 + 4, y observa que la segunda integral es directa, y la expresión de su solución general es: (1/2)*arctan(w/2) + C).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/1/20Te ayudamos con las ecuaciones de los conjuntos de nivel en los dos primeros.
17)
Tienes la expresión de una función de dos variables:
f(x,y) = x2 + x*y;
luego, planteas la ecuación general de las curvas de nivel de esta función, y queda:
x2 + x*y = c, con c ∈ R,
restas x2 en ambos miembros, y queda:
x*y = c - x2,
divides por x en ambos miembros, y queda:
y = c/x - x, con x ≠ 0, c ∈ R.
23)
Tienes la expresión de una función de tres variables:
f(x,y,z) = x*y + y*z;
luego, planteas la ecuación general de las superficies de nivel de esta función, y queda:
x*y + y*z = c, con c ∈ R,
restas x*y en ambos miembros, y queda:
y*z = c - x*y,
divides por y en todos los términos, y queda:
z = c/y - x, con y ≠ 0, c ∈ R.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 19/1/20Te ayudamos con las ecuaciones de las curvas de nivel.
26)
Tienes la expresión de una función de dos variables:
f(x,y) = Máx(|x|,|y|);
luego, planteas la ecuación general de las curvas de nivel de esta función (observa que esta función toma valores positivos), y queda:
Máx(|x|,|y|) = c, con c ∈ R, c ≥ 0.
Luego, tienes dos opciones:
1°)
si |x| ≥ |y| (observa que corresponde a las regiones definidas: R1a: -x ≤ y ≤ x ∧ x ≥ 0, y R1b: x ≤ y ≤ -x ∧ x ≤ 0).
entonces tienes que la ecuación general de las curvas de nivel de la función es:
|x| = c,
que para cada una de las regiones quedan expresadas:
x = c, para la región R1a,
-x = c, para la región R1b;
2°)
si |y| > |x| (observa que corresponde a las regiones definidas: R2a: -y < x < y ∧ y > 0, y R2b: y < x < -y ∧ x < 0).
entonces tienes que la ecuación general de las curvas de nivel de la función es:
|y| = c,
que para cada una de las regiones quedan expresadas:
y = c, para la región R2a,
-x = c, para la región R2b.
Espero haberte ayudado.
-


Antonius Benedictus
el 19/1/20Atento: Para que un subconjunto de un espacio vectorial sea subespacio de él, ha de estar caracterizado por
Ser un conjunto generado linealmente por ciertos vectores.
O bien, venir dado por un sistema de una o varias ECUACIONES LINEALES (de primer grado) HOMOGÉNEAS (con término independiente 0). Éstas son sus ecuaciones implícitas o cartesianas.
-


Antonio Silvio Palmitano
el 19/1/2019)
Tienes la expresión de la solución única del sistema: S = { (2,0,-1) };
luego, reemplazas las coordenadas del punto en el sistema de ecuaciones de tu enunciado, resuelves términos, cancelas términos nulos, y queda:
2 = 2, que es una Identidad Verdadera,
2 + b = 3, y de aquí despejas: b = 1 (1),
3 = 3, que es una Identidad Verdadera;
luego, reemplazas el valor remarcado y señalado (1) en el sistema de ecuaciones de tu enunciado (observa que indicamos a las incógnitas: x, y, z), y queda:
2*x - a*y + 2*z = 2,
x + y - z = 3
2y - 3z = 3,
que es un sistema de tres ecuaciones lineales, de primer grado y con tres incógnitas;
luego, planteas la expresión de la matriz del sistema (recuerda que sus elementos son los coeficientes de las incógnitas), y queda:
A =
2 -a 2
1 1 -1
0 2 -3;
luego, planteas la expresión del determinante de la matriz del sistema, lo desarrollas (por ejemplo según su tercera fila, o por medio de la Regla de Sarrus), y queda:
|A| = (-6 + 0 + 4) - (0 + 3*a - 4), reduces términos semejantes en los agrupamientos, cancelas términos nulos, y queda:
|A| = -2 - (3*a - 4), distribuyes el segundo término, reduces términos semejantes, y queda:
|A| = -3*a + 2 (2).
Luego, planteas la condición correspondiente a compatibilidad determinada de un sistema "cuadrado", y tienes la ecuación negada:
|A| ≠ 0, sustituyes la expresión señalad (2) en el primer término, y queda:
-3*a + 2 ≠ 0, y de aquí despejas: a ≠ 2/3.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 19/1/2020)
Considera un elemento del conjunto solución, por ejemplo al valor del parámetro λ = 0: (2,0,-1,0), reemplazas las coordenadas de este punto en el sistema de ecuaciones de tu enunciado, resuelves términos, cancelas términos nulos, y queda:
0 = 0, que es una Identidad Verdadera,
0 = -k2 + 1 (1),
-(k + 1) = -k - 1, que es una Identidad Verdadera.
Luego, sumas k2 en ambos miembros de la ecuación señalada (1), y queda:
k2 = 1, aquí extraes raíz cuadrada en ambos miembros, y tienes dos opciones:
k = -1 o k = 1.
Luego, considera cada opción por separado:
1°)
k = -1,
reemplazas este valor en el sistema de ecuaciones de tu enunciado, resuelves coeficientes, cancelas términos nulos, y queda (observa que indicamos a las incógnitas: x, y, z, w):
x - y + 2*z = 0, de aquí despejas: z = -(1/2)*x + (1/2)*y (1a),
2*w = 0, de aquí despejas: w = 0 (1b),
4*w = 0, de aquí despejas: w = 0 (1b),
luego planteas la expresión general de un elemento del conjunto solución, y queda:
u = < x ; y ; z ; w >, sustituyes las expresiones señaladas (1a) (1b), y queda:
u = < x ; y ; -(1/2)*x + (1/2)*y ; 0 >, descompones como sumas de vectores según las incógnitas, y queda.
u = < x ; 0 ; -(1/2)*x ; 0 > + < 0 ; y ; (1/2)*y ; 0 >, extraes factores escalares en los términos, y queda:
u = x* < 1 ; 0 ; -1/2 ; 0 > + y*< 0 ; 1 ; 1/2 ; 0 >,
y tienes que este elemento no pertenece al conjunto solución M que tienes en tu enunciado, ya que los elementos de dicho conjunto dependen de un solo parámetro (λ), mientras que el elemento general u depende de dos parámetros (x e y), que corresponden a los vectores:
< 1 ; 0 ; -1/2 ; 0 > y < 0 ; 1 ; 1/2 ; 0 >, que son linealmente independientes (te dejo la tarea de demostrarlo,
por lo que puedes concluir que esta opción no es válida para este problema;
2°)
k = 1,
reemplazas este valor en el sistema de ecuaciones de tu enunciado, resuelves coeficientes, cancelas términos nulos, y queda (observa que indicamos a las incógnitas: x, y, z, w):
x - y + 2*z = 0 (2a),
2*w = 0, de aquí despejas: w = 0 (2b),
2*z + 4*w = -2 (2c),
luego reemplazas el valor señalado (2b) en la ecuación señalada (2c), resuelves términos, cancelas el término nulo, y luego despejas: z = -1 (2d),
luego reemplazas el valor señalad (2d) en la ecuación señalada (2a), resuelves el término numérico, y luego despejas: x = y + 2 (2e),
luego planteas la expresión general de un elemento del conjunto solución, y queda:
u = < x ; y ; z ; w >, sustituyes las expresiones señaladas (2b) (2d) (2d), y queda:
u = < y + 2 ; y ; -1 ; 0 >, descompones como sumas de vectores según la incógnita y los valores constantes, y queda.
u = < y ; y ; 0 ; 0 > + < 2 ; 0 ; -1 ; 0 >, extraes el factor escalar en el primer término, y queda:
u = y* < 1 ; 1 ; 0 ; 0 > + < 2 ; 0 ; -1 ; 0 >, con y ∈ R,
y tienes que este elemento sí pertenece al conjunto solución M que tienes en tu enunciado (observa que hemos obtenido la misma expresión general de los elementos del conjunto M, con la salvedad que el parámetro nos quedó indicado con y),
por lo que puedes concluir que la opción: k = 1 sí es válida para este problema.
Espero haberte ayudado.