-


Antonio Silvio Palmitano
el 17/1/20Tienes una ecuación cartesiana implícita del primer plano, al cuál pertenecen los puntos buscados:
3*x - 2*y + z = 4 (1).
Has planteado correctamente la ecuación del segundo plano, junto con la expresión de su vector normal y su módulo:
-2*x - 6*y + 3*z + 3 = 0 (2), cuyo vector normal es: n2 = < -2 ; -6 ; 3 >, cuyo módulo es: |n2| = 7.
Luego, planteas la expresión general del un punto perteneciente al primer plano, y queda: P1(X,Y,Z),
y observa que debe verificar la ecuación de su plano señalada (1), por lo que sustituyes las expresiones de sus coordenadas, y queda:
3*X - 2*Y + Z = 4, y de aquí despejas: Z = 4 - 3*X + 2*Y (3).
Luego, planteas la expresión de la distancia entre el punto P1(X,Y,Z) y el segundo plano, que debe ser igual a dos según tu enunciado, y queda:
2 = |-2*X - 6*Y + 3*Z + 3|/7, multiplicas por 7 en ambos miembros, y queda:
14 = |-2*X - 6*Y + 3*Z + 3|, aquí sustituyes la expresión señalada (3), y queda:
14 = |-2*X - 6*Y + 3*(4 - 3*X + 2*Y) + 3|, distribuyes el último término y reduces términos semejantes en el argumento del valor absoluto, y queda:
14 = |-11*X + 15|;
luego, de acuerdo con la definición de valor absoluto, tienes dos opciones:
1°)
-14 = -11*X + 15, y de aquí despejas: X = 29/11 (4),
reemplazas el valor señalado (4) en la ecuación señalada (3), y queda:
Z = -43/11 + 2*Y, restas 2*Y en ambos miembros, y queda: -2*Y + Z = -43/11 (5);
luego, tienes un conjunto de puntos cuya gráfica es la recta intersección de los planos cuyas ecuaciones tienes indicadas (4) (5), cuyos vectores normales son:
N1 = < 1 ; 0 ; 0 > y N2 = < 0 ; -2 ; 1 >, cuyo producto vectorial es el vector director de la recta: ur1 = < 0 ; -1 ; -2 >,
luego, signas el valor: Y = 0, lo reemplazas en la ecuación señalada (5), resuelves, y queda: Z = -43/11, y junto con el valor señalado (4), tienes las coordenadas de un punto perteneciente a la recta intersección: A1(29/11,0,-43/11),
luego, con las componentes del vector director, y del punto perteneciente a la recta, planteas sus ecuaciones cartesianas paramétricas, y queda:
X = 29/11,
Y = -λ,
Z = -43/11 - 2*λ,
con λ ∈ R.
2°)
14 = -11*X + 15, y de aquí despejas: X = 1/11 (4*),
reemplazas el valor señalado (4*) en la ecuación señalada (3), y queda:
Z = 41/11 + 2*Y, restas 2*Y en ambos miembros, y queda: -2*Y + Z = 41/11 (5*);
luego, tienes un conjunto de puntos cuya gráfica es la recta intersección de los planos cuyas ecuaciones tienes indicadas (4*) (5*), cuyos vectores normales son:
N1 = < 1 ; 0 ; 0 > y N2 = < 0 ; -2 ; 1 >, cuyo producto vectorial es el vector director de la recta: ur1 = < 0 ; -1 ; -2 >,
luego, signas el valor: Y = 0, lo reemplazas en la ecuación señalada (5*), resuelves, y queda: Z = 41/11, y junto con el valor señalado (4*), tienes las coordenadas de un punto perteneciente a la recta intersección: A2(1/11,0,41/11),
luego, con las componentes del vector director, y del punto perteneciente a la recta, planteas sus ecuaciones cartesianas paramétricas, y queda:
X = 1/11,
Y = -μ,
Z = 41/11 - 2*μ,
con μ ∈ R.
Tal como indica el colega César, tienes remarcadas las dos rectas, que son paralelas a la recta que es intersección de los dos planos que tienes planteados, y que distan dos unidades de ella.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/1/20Vamos con una orientación.
Has planteado correctamente la separación de variables, y te ha quedado la ecuación diferencial:
dy/(1+y2) = tan(t)*dt,
expresas a la tangente en función del seno y del coseno, y queda:
dy/(1+y2) = [sen(t)/cos(t)]*dt,
integras en ambos miembros, observa que en el segundo miembro debes aplicar la sustitución, o cambio de variable: u = cos(t), y queda:
arctan(y) = -ln(|cos(t)|) + C (1);
luego, a partir de la condición inicial de tu enunciado: y(0) = √(3), tienes los valores: t = 0, y = √(3), los reemplazas en la ecuación señalada (1), resuelves (observa que elegimos valores del primer cuadrante), y queda:
π/3 = -0 + C, cancelas el término nulo, y luego despejas:
C = π/3,
que es el valor particular de la constante de integración para la condición inicial de tu enunciado;
luego, reemplazas el valor remarcado en la ecuación señalada (1), y queda:
arctan(y) = -ln(|cos(t)|) + π/3,
compones en ambos miembros con la función tangente, y queda:
y = tan(-ln(|cos(t)|) + π/3),
que es la expresión explícita de la solución general de la ecuación diferencial de tu enunciado, con la condición inicial indicada.
Espero haberte ayudado.
-
me podría decir como resolver x^2 mayor o igual que x


Antonio Silvio Palmitano
el 17/1/20Tienes la inecuación:
x2 ≥ x, restas x en ambos miembros, y queda:
x2 - x ≥ 0, extraes factor común en el primer miembro, y queda:
x*(x - 1) ≥ 0,
por lo que tienes que la multiplicación de los dos factores del primer miembro debe ser ampliamente positiva, por lo que tienes dos opciones:
1°)
los dos factores son negativos a la vez, por lo que puedes plantear que deben verificar las inecuaciones:
x ≤ 0, que corresponde al intervalo: (-∞;0],
x - 1 ≤ 0, aquí sumas 1 en ambos miembros, y queda: x ≤ 1, que corresponde al intervalo: (-∞;1],
por lo que tienes que los elementos que verifican las dos inecuaciones cumplen la condición: x ≤ 0, y pertenecen al intervalo: I1 = (-∞;0];
2°)
los dos factores son positivos a la vez, por lo que puedes plantear que deben verificar las inecuaciones:
x ≥ 0, que corresponde al intervalo: [0;+∞),
x - 1 ≥ 0, aquí sumas 1 en ambos miembros, y queda: x ≥ 1, que corresponde al intervalo: [1;+∞),
por lo que tienes que los elementos que verifican las dos inecuaciones cumplen la condición: x ≥ 1, y pertenecen al intervalo: I2 = [1;+∞).
Luego, con las condiciones que tienes remarcadas, y con los intervalos que tienes remarcados, tienes dos opciones para presentar el conjunto solución de la inecuación cuadrática de tu enunciado:
S = { x ∈ R ; x ≤ 0 ∨ x ≥ 1 },
S = I1 ∪ I2, de donde tienes: S = (-∞;0] ∪ [1;+∞).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/1/20Tienes la ecuación diferencial:
y' = √(y+1)*cost (1),
con la condición inicial:
y(π) = 0 (2).
Luego, expresas al primer miembro de la ecuación señalad (1) como un cociente entre diferenciales, separas variables, y queda:
dy/√(y+1) = cost*dt,
multiplicas por 1/2 en ambos miembros, y queda:
dy/[2*√(y+1)] = (1/2)*cost*dt,
integras en ambos miembros, y queda:
√(y+1) = (1/2)*sent + C (3);
luego, con la condición inicial señalada (2) tienes los valores: t = π, y = 0, reemplazas, resuelves términos, y queda:
1 = 0 + C, cancelas el término nulo, y luego despejas:
C = 1,
que es el valor particular de la constante de integración para la condición inicial indicada en tu enunciado;
luego, reemplazas este valor remarcado en la ecuación señalada (3), y quead:
√(y+1) = (1/2)*sent + 1,
elevas al cuadrado en ambos miembros, y queda:
y + 1 = [(1/2)*sent + 1]2,
restas 1 en ambos miembros, y queda:
y = [(1/2)*sent + 1]2 - 1,
que es una expresión explícita de la solución particular de la ecuación diferencial con condición inicial, que tienes en tu enunciado.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/1/20Vamos con una orientación.
Has planteado bien, aunque en forma algo confusa, la separación de variables, y te ha quedado la ecuación diferencial:
(2*y + 1)*dy = (3*t2 + 4*t + 2)*dt,
integras en ambos miembros, simplificas en cada término, y queda:
y2 + y = t3 + 2*t2 + 2*t + C,
sumas 1/4 en ambos miembros, y queda:
y2 + y + 1/4 = t3 + 2*t2 + 2*t + C + 1/4,
factorizas el trinomio cuadrado perfecto en el primer miembro, expresas a la suma de constantes del segundo miembro (C + 1/4) como una nueva constante, y queda:
(y + 1/2)2 = t3 + 2*t2 + 2*t + k, con k ∈ R,
y luego puedes continuar la tarea.
Espero haberte ayudado.
-
en la derivada arcsec(x+1/x-1)
me tranque este paso y no se lllegar a la solucion
2/(x-1) a 2 solo este
sobre
x +1/x-1) todo a la 2 /raiz de 4x/x+1)a la 2 solo este
les pido esta algebra si pueden no hacerla por los programas pues yo lo que no entiendo es solo como llegar al resultado
que es 1/x-1 por raiz de x










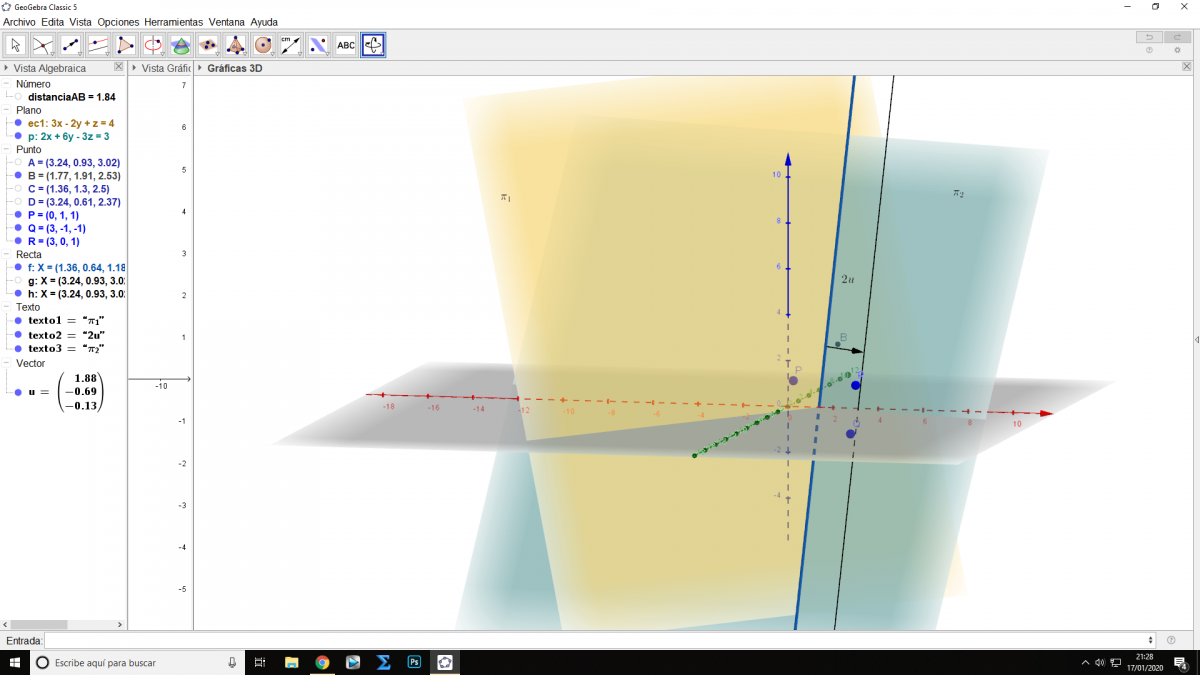























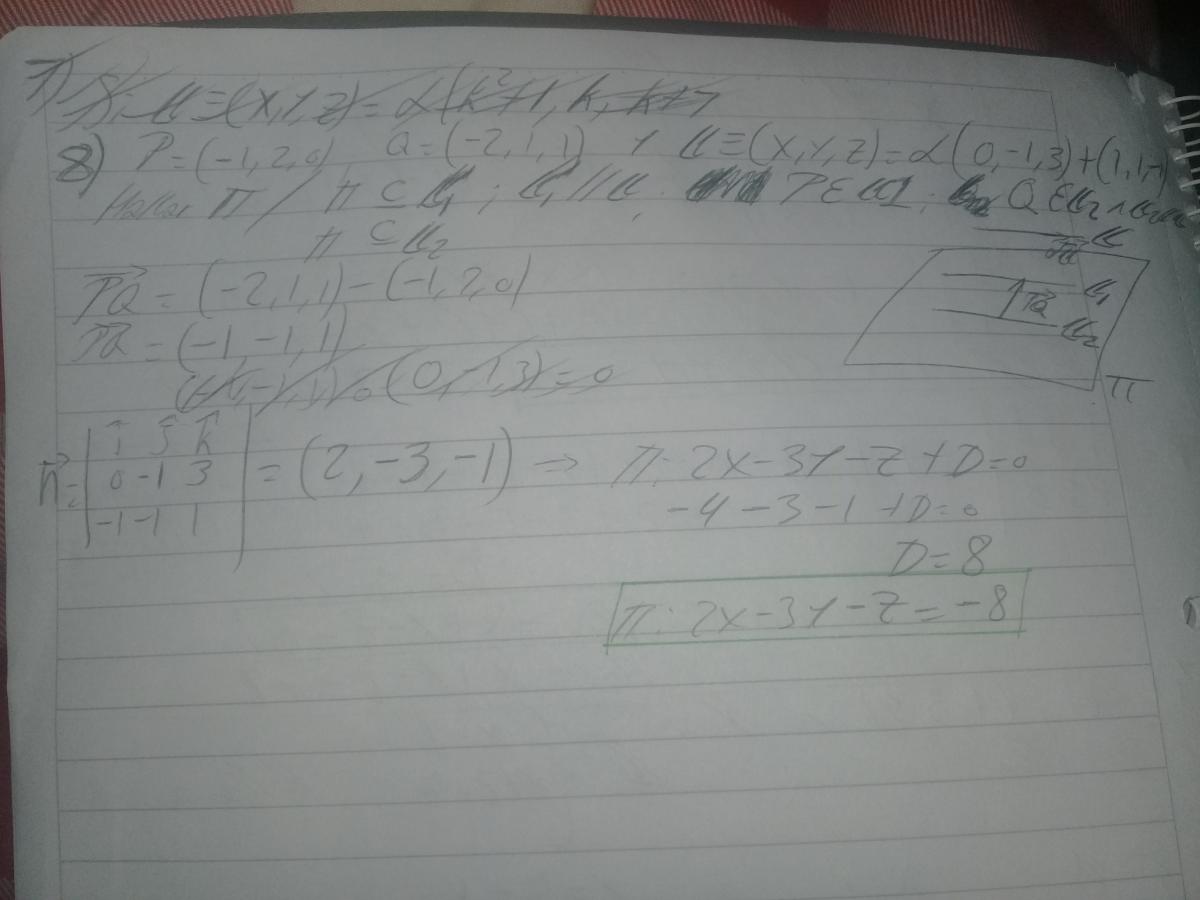 quisiera saber si esta bien,tanto la interpretracion geometrica como la analitica.
quisiera saber si esta bien,tanto la interpretracion geometrica como la analitica.

