-

Antonio
el 17/1/20a) 2t/(1+t2)=1=> t=1 => al año
b) b'(t)=0 => t=±1 => al año hay un extremo
b''(1)<0 => en t=1 hay un Máximo => los beneficios máximos se obtienen al cabo de un año
el mínimo lo tiene en t=0 => los beneficios mínimos se obtienen el primer día
los beneficios crecen desde el principio hasta un año y decrecen a partir de ahí
c) limx→+∞b(t)=0 => los beneficios van mermando hasta que desaparecen
-
Como derivar, por favor, es que no me salen;
1)) x²*sentgx
2)) ln(tgx)²
3)) sen²(e^sen²t)


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Ejercicio 11. Dados los puntos P = (1, −1, 1), Q = (2, 0, 3) y R = (0, 1, 2), calcular el perí-
metro, los ángulos interiores y el área de:
a) el paralelogramo de lados PQ y PR.
b) el triángulo PQR. Decidir si es un triángulo isósceles, equilátero o escaleno. preciso resolucion, desde ya. Gracias
-


Alejandro Legaspe
el 17/1/20Hacer todo el problema por inducción me parece un poco tortuoso,no sé si te sirva,pero podrías probar que para cualquier n, n∧7-n es divisible por 2,3 y 7,es decir,hacer tres pequeños problemas (Algunos pueden salir por inducción)
Probemos entonces que para cualquier n, 2 divide a n∧7-n,observa que si n es par,n∧7 también lo es, es decir si n=2k para alguna k∈ℤ,entonces n∧7=(2k)∧7 que también es par,es claro entonces que n∧7-n es par.Ahora si n es impar,es decir n=2k+1 para algun k∈ℤ,observa que n∧7=(2k+1)∧7=(2k)∧7+(2k)∧6+...+1
Así,podemos escribir
n∧7=(2k+1)∧7=(2k)∧7+(2k)∧6+...+1=2t+1 para algún t∈ℤ,es decir que n∧7 es impar también,así,hemos probado que para cualquier n natural,n∧7 y n tienen la misma paridad,así n∧7-n es siempre par.
Para probar que n∧7-n es divisible por 3,observa primero que n³-n es divisible por 3 (esto se puede probar por inducción) hagamos esta prueba,ahora es inmediata por el pequeño teorema de Fermat.
Es claro que si n=0, n³-n es divisible por 3,ahora para n>0 supon que 3 divide a n³-n,ahora bien (n+1)³-(n+1)=n³+3n²+3n+1-n-1=n³+3n²+2n=n³-n+3n²+3n=n³-n+3(n²+n)
Aplicando la hipotesis de inducción,sabemos que 3z= n³-n,para algún z∈ℤ,así,tenemos
(n+1)³-(n+1)=3z+3(n²+n)=3(z+n²+n) es decir,3 divide a n³-n para cualquier natural n.
Ahora bien,volviendo al problema de probar que n∧7-n es divisible por 3 observa que
n∧7-n=n(n∧6-1)=n(n²-1)(n∧4+n²+1)=(n³-n)(n∧4+n²+1)
Y como n³-n es divisible por 3,entonces también lo es n∧7-n para todo n natural.
Para probar que n∧7-n es divisible por 7 igualmente puedes hacerlo por el pequeño teorema de Fermat,pero si no te agrada,puedes intentarlo por inducción.primero observa que si n=0,es claro que n∧7-n es divisible por 7,ahora bien, supon que 7 divide a n∧7-n y probemos que (n+1)∧7-(n+1) es divisible por 7,observa que,no hace falta hacer las cuentas,pero vamos a hacerlas
(n+1)∧7=n∧7+7n∧6+21n∧5+35n∧4+35n³+21n²+7n+1
Así (n+1)∧7-(n+1)=n∧7+7n∧6+21n∧5+35n∧4+35n³+21n²+6n=n∧7-n+7n∧6+21n∧5+35n∧4+35n³+21n²+7n=n∧7-n+7(n∧6+3n∧5+5n∧4+5n³+3n²+n)
Por hipotesis de inducción,sabemos que existe p∈ℤ tal que 7p=n∧7-n,así,tenemos que:
(n+1)∧7-(n+1)=7p+7(n∧6+3n∧5+5n∧4+5n³+3n²+n)=7(p+n∧6+3n∧5+5n∧4+5n³+3n²+n)
Es decir,7 divide a (n+1)∧7-(n+1) así, 7 divide a n∧7-n para cualquier n natural.
Como 2,3 y 7 dividen a n∧7-n,es claro que 42 también lo divide.
Cualquier duda,quedo atento
-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola Unicoos!
Alguien me puede ayudar... tengo una pequeña duda
al calcular la inversa de la función
y=-x+2 despejo la x
y-2=-x
-y+2=x cambio las variables
-x+2=y
Y me da lo mismo
Es correcto lo que hice?
Desde ya muchas gracias!!!
Saludos
Leily



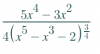




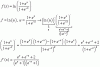













 r3,por lo tanto resto la dimension con las ecuaciones que me restringen,2 parametros,esta correcto?.
r3,por lo tanto resto la dimension con las ecuaciones que me restringen,2 parametros,esta correcto?.

