¡UPS! Para ver vídeos en la web debes estar registrado, es totalmente gratuito.
Recuerda además que sólo por ser unicoo, GRATIS, podrás dejar tus dudas en los foros de beUnicoos, acumularás energy y help points y ganarás decenas de medallas. Registrarte solo te llevará unos segundos. Nosotros somos unicoos ¿y tú? #nosvemosenclase
Area entre funciones 01
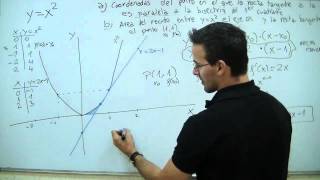
Haremos el segundo ejercicio de selectividad de junio de 2010 de Matemáticas aplicadas a las Ciencias Sociales. En este caso, nos piden hallar el area entre dos funciones utilizando integrales definidas. Empezaremos con la representacion grafica de la parabola (ecuacion de segundo grado)
* Para utilizar tu mochila o guardar tu progreso y acumular energy points debes ser usuario registrado. Regístrate o inicia sesión
Material adicional
* Los materiales marcados con el símbolo de la estrella () sólo serán accesibles para usuarios PRO. Conviértete en PRO
Foro de preguntas y respuestas
-
Una pregunta, al decirte que la recta es tangente a la funcion en el P(1,1) no debes de saber ya que el punto de interseccion entre ambas es en ese punto?un saludo
-
Profe una duda. En el caso de que no nos hayan dado el dato del eje Ox, al calcular el área se hace igual? En el integral también? Lo pregunto más que nada por la parte que se hace la función de arriba menos la de abajo. Saludos.
-
Uf en este video te has rallao mucho, el punto ese no se de dónde te lo has sacado, la tangente a una curva solo tiene un punto en común con la curva, por eso te da ambas veces el (1,1) jaja. Y para el área basta con hacer la integral entre 0 y 1 de x² y restarle la integral entre 0.5 y 1 de 2x-1.
-
Hola, en el minuto 5'50'' creo que no te hace falta hallar el punto de corte de la recta con la curva, porque la recta es precismente la tangente a la curva en el punto (1,1) que te pedía el enunciado, por lo tanto, el único punto de contacto de la recta y la curva será dicho punto (1, 1). Lo que pasa es que al dibujarlas a mano no sale exacto y puede llegar a despistar. De todas formas, el sistema de ecuaciones que has hecho te sirve para comprobar que no te has equivocado y efectivamente esa recta es tangente a la curva en el punto (1,1). Enhorabuena por la página, me encantan tus vídeos.
-
CUIDADO TODO EL MUNDO! cuando en el minuto 5:33 David marca el punto de corte, creo que lo indica en un punto que no toca! muchísimas gracias David por este vídeo! pero he pensado en escribirlo por si alguien se lo preguntaba, el hecho de que estuviera allí marcado, que es lo que a mi me ha pasado:) UN GRAN VÍDEO! MUCHAS GRACIAS! SIGUE ASÍ! ERES ESTUPENDO!
-
hola tengo una duda, ¿ por qué en la primera parte del area x^2 - g(x) este último tiene valor 0 y en la segunda parte g(x) es igual a 2x-1?