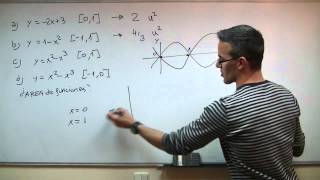Acceder / Registrarse
Matemáticas 2º Bachiller Integral definida - Área de una función y volumen de revolución

Regístrate gratis para ver este vídeo

Es gratuito y se tarda menos de un minuto. Guarda tu progreso, acumula energy points y accede a todas las lecciones.

Crear cuenta gratisIniciar sesión

Volumen de revolución de un cono

Aplicaremos el uso de las integrales al cálculo de VOLÚMENES de REVOLUCIÓN para deducir la fórmula del volumen de un CONO de altura H y radio R. Definida la función a revolucionar con respecto al eje x, una funciion afín que define una área triangular entre los puntos (0,R) y (H,0), obtendremos que el volumen de un CONO, revolucionando la función con respecto al eje de abscisas (eje OX).

🎒 CC
0/ 657

* Para utilizar tu mochila o guardar tu progreso y acumular energy points debes ser usuario registrado. Regístrate o inicia sesión

* Los materiales marcados con el símbolo de la estrella () sólo serán accesibles para usuarios PRO. Conviértete en PRO

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos
Lección anterior:
Integrales trigonométricas
Lección siguiente:
Teorema fundamental del cálculo

Integral definida - Área de una función y volumen de revolución