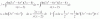-


David
el 26/9/16Yo haría cambio de variable t=3x³-6x²..... dt=(9x²-12x).dx... dt=3x.(3x-4).dx... dx= dt/(3x.(3x-4))
Como 3x³-6x²= 3x².(x-2)... puedes tambien decir que t=3x².(x-2)...
Sustituimos dx y t=3x³-6x². Te queda... ∫ [lnt . (3x-4)/(x.(x-2)] [dt/(3x.(3x-4))] = ∫ [lnt /(3x²(x-2))] dt .. Como el denominador es igual a lo que obtuvimos para t... te quedará ∫ (lnt /t).dt
Y esa integral se hace por partes, muy parecida a esta... Integral por partes Lnx siendo u=lnt y dv=(dt/t)... de donde du= (1/t). dt y v=lnt...
Te sugiero los videos de cambio de variable... Integrales con cambio de variable -
 Buenas, me da como resultado 1280 Pi
Buenas, me da como resultado 1280 Pi
Pero en el solucionario sale 2080 Pi
Estoy yo mal o es el solucionario?

Lucas
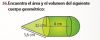
el 26/9/16Zero...
Altura del cilindro es 14m.
El volúmen del cuerpo es:
V=volúmen del cono + volúmen del cilindro.
Ahora
Vcilindro= pi . r^2 . h
Vcilindro= pi . (8m)^2 . 14m
Volúmen cono:
Vcono= pi . r^2 . h/3
Vcono= pi. (8m)^2 . 18m / 3
Volúmen total
Vt= Vcilindro + Vcono
Si la altura total 32m y el cono tiene una altura de 18m, entonces el cilindro tiene 14m.
Éxitos.
-


Lucas
el 26/9/16Zero.
El volúmen de ese cuerpo es:
V = Volúmen del cono + Volúmen del cilindro + Volúmen de la semi esfera
El área del cuerpo es:
A=Área del cono + Área del cilindro + Área de la semi esfera.
Cono:
V= pi . r^2 . h /3
A= pi . r. (g + r)
Cilindro:
V= pi . r^2 . h
A= 2 . pi. r . (h+r)
Semiesfera:
V= 2/3 . pi. r^3
A= 2 . pi. r^2
Según tu ejercicio,
r= 3,5cm
g=5,6cm
h cilindro=4cm
Intenta hacerlo, cualquier duda, pregunta.
Éxitos!
-


Mariam
el 26/9/16Mira, la relación que existe entre el ancho del rectángulo y la altura del cilindro es que ambos son iguales.
Respecto al largo y el radio de la base es que el largo es igual a 2•π•r ya que esta es la fórmula de la circunferencia de un circulo, y como la base es circular y la etiqueta rodea el cilindro entonces el largo es igual a la circunferencia de la base.
-
Me pueden ayudar con este demostración:. Sean los vectores a,b,c,d,e en el Espacio R^3, demostrar que:
[abc][ade]=[abd][ace]-[abe][acd]
-
Hola que tal tengo una duda con este problema de recta ya que no se si mi ecuacion si es la correcta dejo fotos de mis procedimientos por si no se ve el problema es el 16 , la ecuacion que según yo es la solución para el problema es la que esta hasta abajo subrayada.




Antonio Silvio Palmitano
el 26/9/16Observa que la ecuación cartesiana implícita que tienes como dato (la llamamos R1) puedes escribirla: 4x - 5y - 6 = 0.
Luego, como piden una recta paralela a ella (llamémosla R2), puedes plantear su ecuación cartesiana implícita: 4x - 5y + d = 0, en la que debemos determinar el valor de la constante d:
Luego, puedes tomar un punto de la recta R1, asignando un valor para x (por ejemplo x = 0), reemplazas en su ecuación, despejas y queda: y = - 6/5, por lo que el punto (lo llamamos P1) tiene coordenadas: P1(0,-6/5).
Luego, planteamos la expresión de la distancia entre el punto P1 y la recta R2, que según el enunciado debe ser igual a 2:
| 4*0 - 5*(-6/5) + d | / V( 4^2 + (-5)^2 ) = resolvemos donde es posible = |6 + d| / V(41) = 2.
Luego, a partir de la última igualdad de la cadena, y de acuerdo con la definición de valor absoluto, tenemos dos opciones.
a) (6 + d) / V(41) = 2, despejamos y queda: d = 2V(41) - 6 = 6,81 (aproximadamente)
b) (6 + d) / V(41) = - 2, despejamos y queda: d = - 2V(41) - 6 = -18,81 (aproximadamente).
Por lo tanto, tenemos dos rectas paralelas a la recta R1 que se encuentran a distancia 2 de ella, y sus ecuaciones cartesianas implícitas quedan:
R2a: 4x - 5y + 6,81 = 0, cuya ecuación cartesiana explícita es: y = (4/5)x + 1,36 (observa que su ordenada al origen es 1,36, aproximadamente);
R2b: 4x - 5y - 18,81 = 0, cuya ecuación cartesiana explícita es: y = (4/5)x - 3,76 (observa que su ordenada al origen es - 3,76, aproximadamente);
y por último la ecuación cartesiana explícita de la recta R1 es: y = (4/5)x - 1,2 (observa que u ordenada al origen es - 1,2).
Por lo tanto, podemos ver que las tres rectas son paralelas con pendiente 4/5 y, al comparar sus ordenadas al origen, vemos que la recta R2b se encuentra "por debajo" de la recta R1, y que la recta R2a se encuentra "por arriba de la recta R1, ambas a dos unidades de distancia de ésta última.
Espero haberte ayudado.
-
Hoola! He intentado hacer estas derivadas, ¿podrían hacer la 10 y la 13 para comparar resultados? Muchas gracias



Antonio Silvio Palmitano
el 26/9/1610) Observa que tienes un cociente, de la forma: y = u/v cuya derivada es: y ' = ( u ´* v - u * v ' ) / v^2 (*), donde tienes:
u = sen(2x+3), aplicas regla de la cadena y tienes: u ' = cos(2x+3) * 2 = 2cos(2x+3)
v = 3cos(x+1), aplicas regla de la cadena y tienes: v ' = 3* ( - sen(x+1) )*1 = -3sen(x+1),
luego solo queda que sustituyas en la expresión de la derivada señalada (*).
13) Aquí comencemos por derivar la potencia de exponente 5, según la regla de la cadena, luego derivamos su argumento (observa que consta de dos términos (y en el segundo de ellos tenemos nuevamente una regla de la cadena).
La expresión de la función es: y = ( 3x + ( cos(2x+1) )^2 )^5, derivamos y queda:
y ' = 5( 3x + ( cos(2x+1) )^2 )^4 * ( 3 + 2cos(2x+1) * ( - sen(2x+1) )*2 ) (observa que podrías seguir haciendo operaciones, pero la derivación ya terminó).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 26/9/16Recuerda las expresiones del volumen de una esfera maciza y del área de una superficie esférica:
V = (4/3)pi*r^3, y para la semiesfera tenemos: Vs = (2/3)pi*r^3
A = 4pi*r^2, y para la semiesfera tenemos: As = 2pi*r^2
A partir de los datos (indicamos diámetro con d y radio con r): r = d/2 = 23/2 = 11,5 (expresado en metros).
Por lo tanto pasamos a responder:
a) Vs = Vs = (2/3)pi*(11,5)^3 (expresado en metros cúbicos).
b) Comenzamos por el área de la superficie que se debe pintar:
As = 2pi*(11,5)^2 (expresada en metros cuadrados);
luego, con las equivalencias entre unidades de medida:
1 cm = 0,01 m, y 1 cm^2 = 0,0001 m^2
1 ml = 0,001 l;,
sabemos que la cantidad de pintura por unidad de área es:
1 cm^2 / 1 ml = 0,0001 m^2 / 0,001 = 0,01 m^2/l.
Por lo tanto, planteamos la proporción (llamamos x a la cantidad de pintura necesaria expresada en litros):
0,01 m^2/l = As/x, y de aquí puedes despejar la incógnita x (recuerda que el área As está expresada en metros cuadrados).
Espero haberte ayudado.


Mariam
el 26/9/16Mira, el área de una esfera es 4π•r2 y la fórmula del volumen es (4/3)•π•r3
Como es una semiesfera entonces quiere decir que es la mitad de una esfera, entonces vamos a sacar el área y el volumen de una esfera normal y el resultado que nos dé lo vamos a dividir entre dos.
Como me dicen que el diámetro es 23 metros entonces el radio será 23/2 metros. (El diámetro es dos veces el radio).
área:
4π•r2 = 4π•(23/2)2
= 4π•(529/4)
= 529π ya que (4/4=1)
Como era una semiesfera entonces el área ser (529/2)π metros2
Volumen: (4/3)•π•r3= (4/3)π•(23/2)3
= (4/3)π•(12167/8)
= (12167/6)π
Al igual que al área tenemos que dividir entre dos, entonces obtenemos que el volumen es de (12167/12)π metros3
Pintura:
Resulta que me dicen que 1cm2 es igual a 1ml y que 1000ml es igual a 1 litro
ademas tenemos que 1m2 es igual a 10000 cm2
Si tenemos que el área son (529/2)π m2 entonces esa área en cm2 es de 2645000π cm2 si retomamos la igualdad anterior, entonces el área equivale a 2645000π ml, ahora dividimos entre 1000 y obtenemos que se necesitan 2645π litros.
-
Tengo dos funciones x(t)= 2t+3, y(t)= t2+3t y me dicen que t esta en el rango -5≤t≤5 como lo hago para obtener las funciones t vs x y t vs y ?


Antonio Silvio Palmitano
el 26/9/16Las expresiones de las funciones x e y en función de t ya las tienes, y su dominio es el intervalo cerrado [-5,5] tal como expresa la doble desigualdad para t.
Observa que x(t) es una expresión lineal de primer grado, por lo que su gráfica es un segmento incluido en una recta (eje de abscisas: Ot, eje de ordenadas: OX), luego su imagen será el intervalo cerrado (evaluamos t para los extremos del intervalo): I = [-7,13].
Observa qu y(t) es una expresión polinómica cuadrática, por lo que su gráfica es un arco incluido en una parábola (eje de abscisas: Ot, eje de ordenadas; OY), luego para establecer su intervalo imagen tenemos que llevar la expresión a su forma canónica:
y(t) = t2 + 3t = sumamos y restamos (3/2)^2 = 9/4 = (t^2 + 3t + 9/4) - 9/4 = factorizamos en el primer término = (t + 3/2)^2 - 9/4.
Luego, a partir del intervalo tenemos:
-5 <= t <=5, sumamos 3/2 en los tres miembros, resolvemos y queda:
-7/2 <= t + 3/2 <= 13/2, elevamos al cuadrado en el miembro central, y observa que la expresión resultante toma valores positivos:
0 <= (t + 3/2)^2 <= 169/4, restamso 9/4 en los tres miembros, resolvemos y queda:
- 9/4 <= (t + 3/2)^2 - 9/4 <= 40, por lo que tenemos que la imagen de la función es el intervalo cerrado: I = [-9/4,,40].
Espero haberte ayudado.