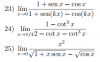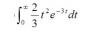Te lo explicamos, Mariam:

:o no conocía eso del coseno :o Mil gracias!! voy a hacerla por mi cuenta a ver si lo entendí bien haha graaciaas

Te va el segundo, Mariam:

Puedes aplicar el criterio que quieras, si con el criterio de la raiz el limite te sale menor que 1 la serie convergera, y si es mayor que uno la serie diverge; el problema sera cuando el limite te de igual a uno, entonces tendras que utilizar otro criterio  como por ejemplo el del cociente.

esta bien entiendo eso pero mi duda es si se pueden aplicar dos criterios al mismo tiempo primero uno y luego el otro 

No tiene ningun sentido, si te sale la solucion bien en uno nose porq quieres utilizar otro, pero si, podrias hacerlo.

Calculamos:

1 ha = 10000 m²

1 hm= 100 m

S= b·h→40000=b·h  (1)

P=2b+2h→1000=2b+2h  (2)

(1)b=40000/h   Sustityendo en (2) tenemos: 1000=2·40000/h+2h=80000/h+2h=(80000+2h²)/h→2h²-1000h+80000=0→h=400 m

b=40000/400=100 m

Respuesta: b=100 m   h= 400 m

saludos.

Tu derivación es perfecta, Nelson. El solucionario está equivocado.

http://www.wolframalpha.com/input/?i=derive+log(cos((x-1)%2Fx)

Te ayudamos, Stefany:

Muchísimas gracias. En mi vida pensé que ese ejercicio fuera tan complicado, estoy haciendo un intensivo y el profesor no explicó ningún ejercicio parecido. Un millón de gracias, muy agradecida 

¿¿??? Dos fracciones equivalentes a que fracción.....?
Amplificación se trata simplemente de multiplicar a numerador y denominador por el mismo numero... 

A ver si la entiendes ahora, diego:

claro hermano muchísimas gracias me ayudo un montón..

Debes aplicar la propiedad de la division de potencias con bases iguales (recuerda que debes restar exponentes), extraer factores constantes, para luego integrar termino a termino.

Espero haberte ayudado.

Bastaria hacer (2-2i)⁵ =-128+128i

Puedes comenzar por dividir por 225 en todos los términos, simplificas y queda:

x^2 / 25 + y^2 / 9 = 1, que es la ecuación de una elipse con centro de simetría en (0,0), eje focal OX, con semieje mayor a = 5 y semieje menor b = 3. Luego, a partir de la relación entre semiejes, tenemos que el semieje focal es: c = 4, por lo que sus focos tienen coordenadas: F1(-4,0) y F2(4,0).

Elijamos el foco F1 para plantear la ecuación general de las rectas que contienen las cuerdas que pasan por él: y = m(x+4).

Luego, nos queda el sistema de ecuaciones para buscar los puntos de intersección entre la elipse y la cuerda general:

9x^2 + 25y^2 = 225

y = m(x +4) (*)

Luego sustituimos la expresión de la segunda ecuación en la primera y queda:

9x^2 + 25 * m^2 * (x + 4)^2 = 225

Luego desarrollas, haces pasaje de término, agrupas términos semejantes y queda:

(9 + 25m^2)*x^2 + 200m^2*x + (400m^2 - 225) = 0,

que es una ecuación polinómica cuadrática (sus coeficientes son: a = 9 + 25m^2, b = 200m^2, c = 400m^2 - 225), aplicas la fórmula resolvente y llegarás a dos expresiones x1 y x2 en función de la pendiente m,

luego reemplazas x1 y x2 en la ecuación señalada (*) y obtendrás sus correspondientes valores y1 e y2, también en función de m.

Por último, solo te quedará plantear que la distancia entre los puntos P1(x1,y1) y P2(x2,y2) es igual a 6:

V( (x2 - x1)^2+ (y2 - y1)^2 ) = 6

haces pasaje de raíz como potencia y queda:

(x2 - x1)^2+ (y2 - y1)^2 = 36.

Observa que cuando reemplaces x1, y1, x2 e y2 por sus expresiones en función de m, te quedará una ecuación con m como  única incógnita, la resuelves, y luego a partir de la ecuación señalada (*) obtendrás las ecuaciones de las dos cuerdas con longitud 6 que pasan por el foco F1.

Espero haberte ayudado.