-
¿Hay alguna diferencia entre el teorema de cauchy para las sucesiones y el echo de que sean convergentes?


Antonius Benedictus
el 11/9/16En un cuerpo de característica distinta de dos cualquier sucesión convergente es de Cauchy. Intuitivamente, esto significa que, si los términos de la sucesión están tan próximos como se quiera del límite, desde uno en adelante, entonces están entre ellos muy próximos.
El recíproco solo se cumple si el cuerpo es completo. En este caso, cualquier sucesión de Cauchy es convergente.
-
Buenas tardes, tengo una duda con esta derivada------sen(xy)+ln(x/y)=e^xy-----
El problema lo tengo con el ln(x/y), nose si lo estoy derivando bien.Tendria que hacer 1/x/y, asi me quede y/x..y recien ahi derivar como una division? o lo dejo simplemente como y/x?
-
¡Buenos días!
Me gustaría saber como puedo determinar el valor de k con tal de que los vectores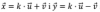 sean perpendiculares, siendo
sean perpendiculares, siendo 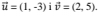
Gracias por adelantado!

Antonio Silvio Palmitano
el 11/9/16Puedes plantear la condición de perpendicularidad entre los vectores x e y: el producto escalar (o) entre ellos debe ser igual a cero:
x o y = 0, reemplazas x = ku+v e y=ku-v por sus expresiones en función de u y v y queda:
(ku + v) o (ku - v) = 0, luego distribuyes (recuerda que el producto escalar es distributivo con respecto a la suma de vectores) y queda:
ku o u - ku o v + v o ku - v o v = 0, luego recuerda que el producto escalar de un vector por sí mismo es igual a su módulo elevado al cuadrado, recuerda que el escalar k puede ser extraído del producto escalar y queda:
k|u|^2 - k*(u o v) + k*(v o u) - |v|^2 = 0, luego, como el producto escalar es conmutativo, tenemos que los dos términos centrales son opuestos, cancelamos y queda:
k|u|^2 - |v|^2 = 0, luego puedes despejar y llegas a:
k = |v|^2 / |u|^2, luego a partir de los datos puedes calcular los módulos de los vectores u y v, reemplazas y queda:
k = 29/10.
Espero haberte ayudado.
-
Buenos días a todos!!
Tengo una duda, sobre como resolver estos problemas, me han ayudado mucho los otros videos, pero con este la verada no doy, espero puedan ayudarme
Gracias a todos y saludos!!
-
Hola a tod@s, resulta que tengo una duda y es como resolver la siguiente ecuación : log(base 3)(3elevado a x -8)= 2-x, espero respuestas¡ , gracias¡


Antonio Silvio Palmitano
el 11/9/16La ecuación es: log( 3^(x-8) ) = 2 - x
Puedes aplicar la propiedad del logaritmo de una potencia (indicamos logaritmo en base 3 como log):
(x-8)*log(3) = 2 - x, luego, como log(3) = 1 queda:
x -8 = 2 - x, haces pasaje de términos, reduces términos semejantes y queda:
2x = 10, luego haces pasaje de factor como divisor y llegas a:
x = 5.
Luego puedes veificar:
log( 3^(5-8) ) = 2 - 5, operamos y queda:
log( 3^(-3) ) = -3, resuelves a la izquierda (recuerda la definición de logaritmo en base tres:
- 3 = - 3.
Espero haberte ayudado.
-
Saludos, Unicoos, tengo una duda respecto a un ejercicio de algebra lineal, trate de hacerlo, por no e podido llegar a la respuesta del libro, puesto que no se de donde salen las fracciones 1/5 y 3/5. espero y me puedan decir, en que me estoy equivocando y como es la forma correcta de resolverlo. gracias de antemano

-
Buenas tardes, ¿Me podrían explicar, por favor, como puedo empezar a resolver estos ejercicios? Resulta que no se muy bien como cojerlos, y una pequeña explicación no me vendría nada mal.
Muchísimas gracias a todos por su ayuda :)
Creo que se pueden entender los ejercicios, ya que están redactados en catalán. Si tienen alguna duda no duduen en consultarme.



Antonio Silvio Palmitano
el 11/9/1616)
Comencemos por trabajar el primer término que es una división entre números complejos, y para ello multiplicamos al numerador y al denominador por el conjugado de éste último:
(3+2i)(1+i) / ( (1-i)(1+i) ) = distribuimos en el numerador y en el denominador y queda:
= (3 + 3i + 2i + 2i^2)/(1 + i - i - i^2) = a partir que i^2 = -1, reemplazamos, reducimos términos semejantes y queda:
= (1 + 5i)/2 = 1/2 + (5/2)i.
Luego, vamos a la expresión inicial (la denominamos z, e indicamos alfa como A) y queda:
z = 1/2 + (5/2)i + Ai agrupamos los dos términos imaginarios y queda:
z = 1/2 + (5/2 + A)i.
Luego, para que z sea un complejo real, su parte imaginaria debe ser nula, por lo que planteamos:
5/2 + A = 0, por último despejamos y tenemos:
A = - 5/2.
17)
Procedemos con la división como en el ejercicio anterior (indicamos alfa como A y beta como B, y llamamos w a la expresión):
w = (3A - 2Bi)(4 +3i) / ((4 - 3i)(4 + 3i) ), distribuimos en el numerador y en el denominador y queda:
w = (12A + 9Ai - 8Bi - 6Bi^2) / ( 16 + 12i - 12i - 9i^2 ), resolvemos i^2 = -1, reducimos términos semejantes y queda:
w = ( (12A + 6B) + (9A - 8B)i ) / 25, distribuimos el denominador y queda:
w = (12A + 6B)/25 + (9A - 8B)i/25.
Luego, para que w sea un número real debe cumplirse:
9A - 8B = 0.
Y para que su módulo sea igual a uno, debe cumplirse (recuerda la expresión del módulo de un número complejo):
V( ((12A + 6B)/25)^2 + ((9A - 8B)/25)^2 ) = 1, hacemos pasaje de raíz como potencia, distribuimos los cuadrados, resolvemos y queda:
(12A + 6B)^2 / 625 + (9A - 8B)^2 / 625 = 1, multiplicamos por 625 en todos los términos y queda:
(12A + 6B)^2 + (9A - 8B)^2 = 625.
Luego, solo queda que resuelvas el sistema de ecuaciones:
9A - 8B = 0.
(12A + 6B)^2 + (9A - 8B)^2 = 625.
Espero haberte ayudado.
-
cuando estoy calculando un limte 0/0, en que casos eso no se considera intederminado... ?????


Antonio Silvio Palmitano
el 11/9/16En este caso se trata de una indeterminación, ya que el numerador tiende a cero y el denominador también tiende a cero.
Luego, recuerda la definición de derivada de una función en un punto, en la que una de las formas de escribirla es:
f ' (a) = Lím(x-->a) ( f(x) - f(a) ) / (x - a).
Observa que en tu ejercicio tienes: f(x) = cosx, cuya derivada es: f ' (x) = - senx, con a = 1, por lo que la expresión corresponde a:
f ' (1) = Lím(x-->1) ( cosx - cos1 ) / (x - 1) = - sen(1).
Observa que puedes confirmar el resultado por medio de la Regla de L'Hôpital.
Espero haberte ayudado.































