-
Tengo una duda con este ejercicio, alguien que me ayude .... (Ecuaciones bicuadraticas )
2X^[4] - X^[2] + 1 = 0

Andrés Alvarado
el 31/7/16Hola guisela en estos casos es recomendable cambiar de variable, en este caso asi:
X^[2]=A por lo tanto X^[4]=A^[2]
Entonces tu ecuacion queda de la forma
2A^[2] - A + 1=0
Donde ahora si puedes realizarlo con la formula general de ecuaciones cuadraticas, y te van a salir valores de A pero recuerda que A=X^[2] Por lo que X es igual a la raiz de A
-
Como se calcularia el rango de esta funcion? 2x-4/raiz cuadrada de 1-x^2 ( dos x menos cuantro sobre raiz de 1-equis cuadrada)
Se que tengo que buscar su inversa ya que el dom de la iversa es el rango de la funcion inicial, pero no puedo llegar a la inversa.Si me pudiesen mostrar como se hace el rango lo agradeceria.
Otra cosa que no tiene nada que ver, a alguien mas no le salen las preguntas que hizo en el panel? Tuve que abrir otra cuenta porque en la anterior, me figura que tengo respuestas por calificar pero me aparece "no se encontraron resultados" en el apartado mis preguntas. -
Ayuda con este ejercicio de coordenadas polares por favor
en el inciso a me pide graficar la ecuación r=secθ entonces hice una tabulacion y luego en el inciso b me pedían hacer lo mismo pero con coordenadas cartesianas, luego viene el inciso c que no he podido resolver porque me piden "determinar la ecuación en coordenadas cartesianas para la gráfica del ejercicio, partiendo de la ecuación parametrica de y". Entonces como pueden ver usando la ecuacion parametrica de x es muy simple porque solo se reemplaza secθ por 1/cosθ y al cancelar queda 1, pero al tratar de hacer lo mismo con la ecuacion parametrica de y no es tan sencillo, no recuerdo bien si lo que me estan pidiendo es llegar a la ecuacion y-y1=m(x-x1) o solo hacer lo que hice con la ecuacion parametrica de x con la de y... help please :c

Antonio Silvio Palmitano
el 31/7/16En ete ejercicio tienes la ecuaciòn:
r = sect (escribimos t indicando "theta")
que por identidad trigonométrica puede escribirse
r = 1/cost
hacemos pasaje de divisor como factor y queda:
r*cost = 1
que pasada a coordenadas cartesianas queda:
x = 1, para todo y perteneciente a R (todos estos pasos los has resuelto correctamente)
Luego, a partir de la expresiòn de y en coordenadas polares:
y = r * sent
sustituimos r y queda:
y = sect * sent
por identidad trigonométrica queda:
y = (1/cost) * sent
y al multiplicar la expresiòn fraccionaria por el segundo factor queda:
y = sent/cost
y por identidad trigonomètrica llegamos finalmenta a:
y = tgt
Por lo tanto, las ecuaciones cartesianas paramétricas de la recta de ecuación x = 1 nos quedan:
x = 1
y = tgt, con t perteneciente a R.
Espero haberte ayudado. -
hola gente, necesito ayuda con el criterio de comparación para estudiar la convergencia de series. alguien tiene material que me pueda ayudar. no logro entender el tema.
-
Me pueden ayudar hacer este ejercicio, peo urgente! por favor
La cantidad de números que comienzan o terminan en 5 y están entre 400 y 600 es
A. 110 B. 120
C.20 D. 100
con procedimiento porfa, y rápido!!!!!!

Antonio Silvio Palmitano
el 30/7/16Puedes plantear N = C + T + CT, donde llamamos:
N cantidad total de números pedidos
C cantidad de números que comienzan en 5 pero no terminan en 5
T cantidad de números que no comienzan en 5 pero si terminan en 5
CT cantidad de números que comienzan en 5 y terminan en 5
Observa que no hay números que cumplan dos o tres de las condiciones (todos cumplen una sola)
Vamos con las cantidades
C = 1*10*9 = 90 observa que tenemos una sola posibilidad para la primera cifra (el 5), diez para la segunda (cualquiera) y nueve para la tercera (cualquiera excepto 5)
T = 1*10*1 = 10 observa que tenemos una sola posibilidad para la primera cifra (el 4), diez para la segunda (cualquiera) y una para la tercera (el 5)
CT = 1*10*1 = 10 observa que tenemos una sola posibilidad para la primera cifra (el 5), diez para la segunda (cualquiera) y una para la tercera (el 5)
Por lo tanto, la cantidad totlal de números pedidos es:
N = 90 + 10 + 10 = 110
Puedes verificar:
Los "números C" son: 500 al 599, quitando 505, 515, 525, ... 585 y 595 (observa que C = 100 - 10 = 90).
Los "números T" son: 405, 415, 425, ... 485 y 495 (observa que T = 10).
Los "números CT" son: 505, 515, 525, ... 585 y 595 (observa que CT = 10).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 30/7/16Observa que algunas intersecciones entre las curvas se visualizan con facilidad:
entre la curva logarítmica y la parábola: punto (1,0)
entre la parábola y la recta paralela al eje de abscisas: punto (0,4) que es el vértice de la parábola
entre la curva logarítmica y la recta paralela al eje de abscisas:
planteamos un sistema de ecuaciones:
y = 4
y = lnx
luego igualamos:
lnx = 4
luego componemos con la función inversa del logaritmo natural y llegamos a:
x = e^4
por lo que el punto de intersección entre la recta paralela al eje de abscisas y la curva logarítmica es: (e^4 , 4).
Ahora sería muy conveniente que grafiques las tres curvas, y que visualices bien la región, que tiene forma parecida a un triángulo con base sobre la recta, con la parábola a la izquierda y la curva logarítmica por la derecha, por lo que nos va a convenir integrar primero x:
límite por la izquierda: y = 4 - 4x^2, despejamos x y queda: x = V(4 - y)
límite por la derecha: y = lnx, despejamos x y queda: x = e^y
Para los límites de y:
el punto más "bajo" de la región tiene ordenada y = 0 (observa que es el punto (1,0)
los puntos más "altos" de la región tienen ordenada y = 4 (observa que son los puntos de la recta comprendidos entre los puntos (0,4) y (e^4,4).
Luego podemos pasar al cálculo del área de la region:
Área de la región = Integral doble (1*dx*dy) = Integral (e^y - V(4 - y))*dy (observa que hemos integrado 1*dx y evaluado entre los límites que hemos determinado)
Solo resta que completes la integral (observa que puedes separar en términos, para el prmero es directa y para el segundo puedes aplicar la sustitución w = 4 -y).
Espero haberte ayudado.
-
hola unicoos, me ayudan a verificar este problema?
los resultados que me dieron fueron los siguientes:
en el inciso a) f(h)=2x (siendo h la cantidad de horas)
b)x=48


Alejandro Legaspe
el 30/7/16Si suponemos que el tercero trabaja "h" horas, el segundo trabajaría 5h/8 y el primero (3/5)(5h/8)=3h/8
Ahora bien, si suponemos que el segundo trabaja "x" horas, entonces x=5h/8
8x=5h
h=8x/5
Luego, como el tercero trabaja "h" horas, entonces trabajara "8x/5" horas
por la tanto, como el primero trabaja 3h/8 de horas, entonces trabajara (3/8)(8x/5)=3x/5 horas
Si sumamos esas "x", entonces obtendremos el total de horas trabajadas por las tres personas en funcion de las horas que trabaja el segundo
3x/5 + x + 8x/5 = x+ 11x/5 = 16x/5
Para el segundo, tenemos que el total de horas es 96, es decir
16x/5=48
x=48(5)/16=(48)(2)(5)/(8)(2)= (8)(6)(5) / (8) = 30=x
Como el primero trabaja 3x/5, entonces (3/5)(30) = (3/5)(6)(5) = 18 horas
-
Buenas noches. Alguien me podria mostrar como se calcula el dominio de esta funcion: y=raiz cuadrada de 4-10^x


Antonio Silvio Palmitano
el 30/7/16Debes plantear la condición correspondiente:
La función tiene esta expresión: f(x) = V(4 - 10^x)
observa que el argumento de la raíz cuadrada debe ser mayor o igual que cero, por lo tanto planteamos:
4 - 10^x >= 0
luego hacemos pasaje de término y queda:
-10^x >= -4
luego multiplicamos en ambos miembros por -1 (recuerda que se invierte el sentido de la desigualdad):
10^x <= 4
luego puedes tomar logaritmos naturales en ambos miembros:
ln(10^x) <= ln4
luego, aplicamos a la izquierda de la igualdad la propiedad del logaritmo de una potencia y queda:
x * ln10 <= ln4
luego, teniendo en cuenta que el logaritmo natural de diez es un número positivo, hacemos pasaje de factor como divisor y llegamos a:
x <= ln4 / ln10
por lo que concluimos que el dominio de la función es D = (-inf ; ln4/ln10] (observa que es un intervalo cerrado por la derecha).
Espero haberte ayudado.



_Thumb.jpg)

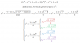




_Thumb.jpg)






_Thumb.jpg)
_Thumb.png)

_Thumb.jpg)
