-
Alguien podria colaborarme con este ejercicios de combinatoria colegio:
En el nuevo congreso, que se subdivide por comisiones, se quiere escoger un presidente y un secretario de un grupo de seis hombres y ocho mujeres. Si se desea que al menos una de estas personas (ya sea el presidente o el secretario) sea una mujer, ¿de cuántas maneras se puede escoger esta dupla?
A. 48 C.56
B. 112 D.152
agradezco cualquier ayuda. saludos -


Francisco Gutiérrez Mora
el 20/7/16Vamos a hacerlo:
sen² x + cos² y =3/4
cos² x - sen² y = 1/4 Sumando miembro a miembro tenemos:
sen² x + cos² x + cos² y -sen² y =1→1 + cos² y - sen² y =1→cos² y =sen² x→cos y = sen y→ sen y =√2/2 ......... cos y =√2/2
sen² x + (√2/2)² = 3/4→sen² x = 3/4-1/2=1/4→sen x = √1/4 = 1/2 →cos x = √3/2
El ángulo y será 45 º y el ángulo x = 30º
Un Saludo.

Antonio Silvio Palmitano
el 20/7/16Observa que puedes sumara las ecuaciones y queda:
(senx)^2 + (cosx)^2 + (cosy)^2 - (seny)^2 = 1
luego, por identidad fundamental para x, y por identidad trigonométrica para y, queda:
1 + cos(2y) = 1
luego aplicamos propiedad cancelativa de la suma y queda:
cos(2y) = 0
luego, por composición de la función coseno con su función inversa arco-coseno tenemos que:
2y = arccos(0)
lo que corresponde a valores de y igual a: pi/2, 3pi/2, 5pi/2, etc, que en general quedan expresados:
2y = pi/2 + n*pi, con n perteneciente al conjunto de los números enteros,
luego despejamos y obtenemos los valores para la incógnita y:
y = (pi/2 + n*pi)/2, con n perteneciente al conjunto de los números enteros,
por último, distribuimos el denominador y llegamos a:
y = pi/4 + n*pi/2, con n perteneciente al conjunto de los números enteros.
Luego puedes restar ambas ecuaciones y queda:
(senx)^2 - (cosx)^2 + (cosy)^2 + (seny)^2 = 1/2
luego, por identidad trigonométrica para x, y por identidad fundamental para y tenemos:
-cos(2x) + 1 = 1/2
luego hacemos pasaje de término, resolvemos y queda:
-cos(2x) = -1/2
luego multiplicamos en ambos miembros por -1 y queda:
cos(2x) = 1/2
luego, por composición del coseno con su función inversa (recuerda también que la función coseno toma valores positivos en el primero y en el cuarto cuadrante) tenemos que:
2x = arccos(1/2)
que nos conduce a:
a) (a partir del ángulo del primer cuadrante)
2x = pi/6 + 2n*pi, con n perteneciente al conjunto de los números enteros,
luego despejamos x, distribuimos el divisor y llegamos a:
x = pi/12 + n*pi, con n perteneciente al conjunto de los números enteros;
b) (a partir del ángulo del cuarto cuadrante)
2x = 11*pi/6 + 2n*pi, con n perteneciente al conjunto de los números enteros,
luego despejamos x, distribuimos el divisor y llegamos a:
x = 11*pi/12 + n*pi, con n perteneciente al conjunto de los números enteros.
Por último, observa que hemos obtenido una fórmula para todos los valores de la incógnita y, pero dos fórmulas para los valores de x, por lo que concluimos:
Conjunto de Soluciónes 1:
x = pi/12 + n*pi, con n perteneciente al conjunto de los números enteros,
y = pi/4 + m*pi/2, con m perteneciente al conjunto de los números enteros. (observa que el número de giros en una fórmula es independiente del número de giros en la otra).
Conjunto de Soluciones 2:
x = 11*pi/12 + n*pi, con n perteneciente al conjunto de los números enteros,
y = pi/4 + m*pi/2, con m perteneciente al conjunto de los números enteros. (observa que el número de giros en una fórmula es independiente del número de giros en la otra).
Hemos resuelto el ejercicio y expresado sus dos posibles conjuntos de soluciones en el conjunto de los números reales (recuerda que una solución es un par de valores, uno para cada incógnita).
Espero haberte ayudado.

Francisco Gutiérrez Mora
el 20/7/16Antonio, tu explicación es impecable, pero a un nivel de bachiller no creo que haga falta tanto razonamiento matemático y tan complicado. Creo que es preferible que el chaval se quede con lo fundamental y reducido al primer cuadrante. Simplemente es mi humilde opinión. Un Saludo.
-
Me dicen que lo resuelva por gauss jordan, la cuestión esta es en que no se si me estoy equivocando o estoy multiplicando mal por el escalar,
Si multiplico
3F1 en un paso y en el segundo paso -F3+F1---->F1
la Fila uno (1) queda Asi
F1= 0 0 0 3 Ι 0
a partir de ahí la matriz ampliada se alarga demasiado y no llego al resultado.
Gracias de Antemano.


Antonio Silvio Palmitano
el 20/7/16Observa que tu sugerencia indica el método de las operaciones elementales, por favor verifica que no te hayan pedido resolver con el método de los pivotes.
Va en la foto la resolución por operaciones elementales que has intentado. Observa que el sistema tiene tres ecuaciones y cuatro incógnitas, y en este caso nos queda indeterminado, ya que admite infinitas soluciones (en otros casos, puede que estemos ante sistemas incompatibles sin solución).
Espero haberte ayudado. -
alguien me puede decir que quiere decir esta frase con respecto al tema de espacios vectoriales:
Como B′ es de cardinal 4 y V es de dimensi´on 4, para demostrar que B′ es base de V , basta con probar que B′ es libre.
EL EJERCICIO ES ESTE

Antonio
el 20/7/16Libre es que ninguno de lo elementos de B' se puede escribir como combinación lineal de los restantes.
Dicho practico, cada elemento debe aportar información, si es mezcla de los otros no aporta nada.
en realidad se demuestra poniendo la ecuación v1=k1 * v2+ k2 * v3 + k3 *v4 si no existen esas tres k para hacer la ecuación verdadera es que son libres
Otra manera de comprobarlo es que el determinante de los coeficientes de las u para cada v no sea cero....
Mario
el 20/7/16cardinal es dimension, cant de vectores linealmente independiente. osea que vas a tener 4 vectores que no se pueden escribir como combinacion lineal de los restantes. entonces era base de tu espacio y generador. ya que tenes 4 elementos en el vector para formar un espacio de 4, pero esto no siempre es cierto.
-
Buenas, no soy capaz de entender para qué sirve hacer Sarrus. Quiero decir, sé hacer el determinante de 3x3 o de 2x2 pero no logro entender el concepto, ¿qué es lo que estamos calculando? ¿Cómo podría aplicarse en el día a día? Muchísimas gracias de antemano.


Adán Sousa Freitas
el 20/7/16Hola.
La regla de Sarrus te permite "resolver" determinantes, ya que, en el fondo, un determinante no es más que una forma de expresar un número, un polinomio, etc. La regla solo es un procedimiento para hayar el valor del determinante. Saber resolver determinantes si es muy importante; ya que es algo muy utilizado; para resolver sistemas de ecuaciones (Kramer), para calcular autovectores y autovalores, para trabajar con formas cuadráticas, determinar el rango de una matriz, discutir sistemas...
Echa un ojo a estos videos; seguro que te ayudan:
Determinante 2x2 - Regla de SARRUS
Determinante 3x3 - Regla de SARRUS
Propiedades de los Determinantes 01
Propiedades de los Determinantes 02
Propiedades de los Determinantes 03
-
Hola, mañana tengo un importante examen de geometría analítica, alguien me podría recomendar algunos trucos para resolver mas rápido los problemas de Geometría analítica (la recta, circunferencia y parábola).

jorge velazquez
el 20/7/16que te aprendáis de memoria la ecuaciones situadas en el origen (ecuación reducida o ordinaria) y utilices traslaciones para que salgan las otras ecuaciones( h,k), hablado de parábola y circunferencia, por otro lado, para la recta solo es necesario saber la formula de la pendiente y punto pendiente, a partir de esta ultima pudes obtener las ecuación de los dos puntos, la general (implícita) y la explicita. y uno de los consejos mas importantes es que leas muy bien el enunciado, y para la ecuación segmentaría de la recta o también conocida como simétrica , un truco muy favorable es que cambies (x,y) por (a,0) en la ecuación explicita y así puedes obtener mas fácil el valor de (a) en la ecuación simétrica, porque (b) te lo da el corte con el eje y (ordenada) de la ecuación explicita y=mx+b espero te ayude amigo .
-
buenas disculpen amigos me podrían ayudar a resolver este ejercicio por favor con aplicación de mínimos y máximos derivando. e intentado pero no me sale el resultado gracias si es posible de antemano
-


Antonio Silvio Palmitano
el 19/7/16Debes tener en cuenta que y es una función de x, que nos conduce a aplicar la regla de la cadena a la derecha de la igualdad.
Comencemos por derivar en ambos miembros de la ecuación:
1 = cos(x + y) * (1 + y ' )
luego distribuimos a la derecha de la igualdad:
1 = cos(x + y) + cos(x +y) * y '
luego hacemos pasaje de término:
1 - cos(x + y) = cos(x + y) * y '
y por últmo un pasaje de factor como divisor:
(1 - cos(x + y)) / cos(x + y) = y ', con la aclaración: cos(x + y) distinto de 0.
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 19/7/16Primero, por favor corrobora que la ecuación diferencial esté escrita en forma correcta.
Luego, tienes:
y = e^(rs), donde r es un número (veremos si es real o complejo), y s es la variable independiente,
luego planteamos las derivadas primera y segunda de la función:
y ' = r * e^(rs)
y ' ' = (r^2) * e^(rs).
luego, sustituimos las tres expresiones en la ecuación diferencial, extraemos factor común y queda:
(r^2 + r + 6) * e^(rs) = 0, luego hacemos pasaje de factor como divisor (observa que el exponencial siempre es distinto de cero porque es mayor estrictamente de cero):
r^2 + r + 6 = 0, que es la ecuación característica de la ecuación diferencial, aplicas la fórmula resolvente y tienes dos soluciones complejas:
r1 = -1/2 + (V(23) / 2)*i y también r2 = -1/2 - (V(23) / 2)*i.
Espero haberte ayudado.




_Thumb.jpg)


_Thumb.png)

_Thumb.png)
_Thumb.jpg)
_Thumb.png)



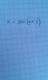
_Thumb.png)



