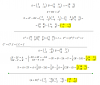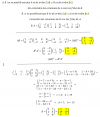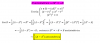-
-
algn me puede ayudar a entender las funciones?
(decreciente, creciente, maximo , minimo , dominio y recorrido) Tengo examen el martes y se me da FATAL
-

 gracias por tu resolucion jose,tengo una consulta en la parte d (pi;pi prima)=2; y ha quedado modulo de (D+5)/3=2,has elegido un valor aleatorio del plano pi?.,supongo y=0 y z=0.esa es mi duda.
gracias por tu resolucion jose,tengo una consulta en la parte d (pi;pi prima)=2; y ha quedado modulo de (D+5)/3=2,has elegido un valor aleatorio del plano pi?.,supongo y=0 y z=0.esa es mi duda.


Jose Ramos
el 16/2/20No. Mi planteamiento es el siguiente:
Elijo un plano paralelo a π, por tanto ha de tener por ecuación -x + 2y + 2z + D = 0. Ahora bien, para que la distancia de dicho plano a π sea 2, utilizo la fórmula que dice que si dos planos son paralelos y sus ecuaciones respectivas son: Ax + By + Cz + D = 0 y Ax + By + Cz + D' = 0, la distancia entre ambos es |D-D'| / √A2+B2+C2 En el problema es |D+5|/3 = 2 (De ahí sale).
-
 4ESO, radián. Adjunto imagen sobre el asunto.
4ESO, radián. Adjunto imagen sobre el asunto.Por favor me podríais aclarar qué significa exactamente el comentario que hace el libro cuando dice literalmente:
“La ventaja principal en la utilización de radianes es que se trata de una unidad natural: no depende de un número arbitrario de divisiones de la circunferencia."
Gracias por vuestra ayuda.


Jose Ramos
el 15/2/20Quédate con la siguiente idea: Si trabajamos los ángulos medidos en grados sexagesimales, hemos de dividir la circunferencia en 360 partes iguales (cada una de dichas partes sería 1º). Esto no deja de ser arbitrario. De hecho existen los grados centesimales que dividen la circunferencia en 400 partes iguales (arbitrario también). El radián no depende de este tipo de divisiones, ya que representa el valor del ángulo que abarca la longitud de arco de circunferencia igual a su radio, por lo que no depende ni de la división de la circunferencia en "trozos", ni del tamaño del radio, porque el ángulo siempre será el mismo aunque el radio aumente. Además, el radian es un número real. Cuando decimos que 180º son π radianes, estamos afirmando que el valor del ángulo que abarca un arco que mide 3,1415... radios (de ahí que se diga que es una medida natural).
Sé que no es fácil pero lo intenté.
Un saludo.