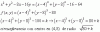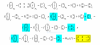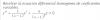-
He pensado en intentar sumar 80 a f(x, y) para así poder hacer algo tipo (a+b)^2 pero no me ha salido nada, entonces si alguien me puede ayudar se lo agradecería.
Dada la funcion f(x, y)= ... Escoged una descripcion adecuada de las curvas de nuvel.
La respuesta es la A.


Jose Ramos
el 10/2/20Hay que igualar la función a k (cortar la superficie con planos de ecuación z = k), de tal modo que queda x2 + y2 -8x -16 y = k. Hacemos una compleción a cuadrados y queda (x-4)2 +(y-8)2 - 16 - 64 = k , de donde:
(x - 4)2 + (y-8)2 = k +80. Cuando k + 80 > 0, k > -80 , se obtiene la ecuación de la circunferencia de centro (4, 8) y radio raíz cuadrada de k + 80. Por tanto la solución es la A.
-
Alguien me puede ayudar con este problema, no me dan los mismos resultados... Gracias.
12. sea ... una aplicación lineasl, la matriz de la cual en las bases B1... y B2...
a) Encontrar la matriz f en las bases canonicas de R^3 y R^2.
b) Encontrar la matriz de f referida en las bases B'1= ... y B'2 =....
c) Encontrar la imagen en las bases B'2 del vector de coordenadas (1,2 ,39^T en la base B1. (T es las transpuesta).