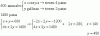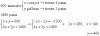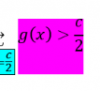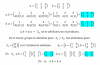-
 hola buenas! me gustaria que me ayudaran con un problema!
hola buenas! me gustaria que me ayudaran con un problema!En una granja entre gallinas y conejos hay un total de 600 animales. Si contaramos sus patas obtendriamos 1480.
¿cuantas gallinas y cuantos conejos hay?
urge un poco de prisa, gracias
-
Alguien me puede explicar un truco o algo para poder saber como funcionan este tipo de problemas? gracias.
Cual de las siguientes es la única lista de composiciones posibles?


Jose Ramos
el 9/2/20La solución correcta es la C.
Tienes que comprobar que el conjunto final de la primera función coincide con el inicial de la segunda. Por ejemplo: g o f (La primera en actuar es f y la segunda es g ). f: R -> R4 g: R4 -> R2 coincide el conjunto final de f (R4) con el inicial de g (R4), por tanto se puede realizar la composición g o f
-


Antonius Benedictus
el 9/2/20Se trata de acotar g(x) inferiormente, con objeto de ver que el cociente g(x)/f(x) es mayor que una cantidad que es tan grande como se desee. Para ello, tomamos un épsilon_2 igual a c/2 (que es positivo) y observamos que, en las proximidades de x=a, es c-c/2<g(x)<c+c/2. De esta desigualdad solo nos interesa la 1ª parte, esto es, que g(x) es > que c/2.
-
 Buenos días. Asintotas en las gráficas de funciones.
Buenos días. Asintotas en las gráficas de funciones. No sé si la pregunta es muy general pero ¿a partir de una función dada se puede saber si la gráfica de la misma presentará algún tipo de asintota (horizontal/oblicua/vertical)?
Adjunto un problema en el que se requiere una función exponencial en la que solo los valores (x,y) positivos tienen sentido, y en cuya gráfica creo que se podría trazar una asíntota horizontal. Gracias por la ayuda.
-
Amigos ayudenme por favor!! Lo publico nuevamente porque no lo he podido resolver!!
En el grupo de las permutaciones de 3 elementos un estudiante realiza los dos productos posibles con las permutaciones de a y b, donde
Luego El conjetura que S3es el menor grupo no abeliano que existe, pues se acuerda que en la unidad anterior se afirma que todos los grupos de orden 4 son conmutativos, su conjetura significa que otro grupo no abeliano, debe tener cardinalidad mayor o igual que la de S3
- Calcular los mencionados productos de a y b.
- Determine si S3 es abeliano o no y por que?
- Diga si es cierto o no que S3 es el menor grupo no abeliano que existe y por que?
-
Hola muy buenas, soy un alumno de matemática computacional y tengo una asignatura que se me atraganta, es algebra lineal. Sabiendo que si dos matrices semejantes tendrán el mismo polinomio característico, me han pedido un ejemplo concreto en el que se pueda comprobar que no se cumple a la inversa. Es decir, que si tienen el mismo polinomio característico no tienen porque ser semejantes. Por favor ayuda, no se ni como empezar a buscar dicho ejemplo!
-
Ayuda con este ejercicio!!
En el grupo de las permutaciones de 3 elementos un estudiante realiza los dos productos posibles con las permutaciones de a y b, donde
Luego El conjetura que S3es el menor grupo no abeliano que existe, pues se acuerda que en la unidad anterior se afirma que todos los grupos de orden 4 son conmutativos, su conjetura significa que otro grupo no abeliano, debe tener cardinalidad mayor o igual que la de S3
- Calcular los mencionados productos de a y b.
- Determine si S3 es abeliano o no y por que?
- Diga si es cierto o no que S3 es el menor grupo no abeliano que existe y por que?


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-

Sebastian Quintero
el 8/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase