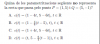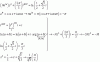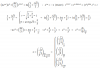-
Alguien me puede ayudar a encontrar las ecuaciones? Solo he podido encontrar la C. Gracias
Cual de las siguientes parametrizaciones siguientes no representa la recta que pasa por los puntos ...?

Sebastian Quintero
el 8/2/20Hay varias formas de resolverlo,yo le propongo que parta de las opciones (es largo,pero supongo que tiene el tiempo )
Recuerde que de las parametricas puede obtener una expresión que involucre solo a x y a y despejando t y usando álgebra elemental...al final llegará a que con una de las parametricas no obtendrá la misma expresión en x e y
-

Sebastian Quintero
el 8/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase
-
A ver si alguien me puede ayudar con este problema, gracias!
Dada las curvas en forma implicita ax^2 + by^2 = ab y bx-y+a = 0 con a, b ∈ R, que representación no es posible?


Antonio Silvio Palmitano
el 8/2/20De la segunda ecuación puedes despejar:
y = b*x + a (1),
que es la ecuación cartesiana explícita de una recta, cuya pendiente es b, y cuya ordenada al origen es a.
Luego, considera cada opción por separado:
A)
Observa que la recta tiene pendiente positiva y distinta de cero, y ordenada al origen negativa y distinta de cero, por lo que puedes plantear (observa que aplicamos propiedades de la función valor absoluto):
b = |b| y a = -|a|;
luego, tienes la primera ecuación de tu enunciado:
a*x2 + b*y2 = a*b, sustituyes expresiones en la primera ecuación de tu enunciado, y queda:
-|a|*x2 + |b|*y2 = -|a|*|b|, divides en todos los términos por -|a|*|b|, y queda:
x2/|b| - y2/|a| = 1,
que es la ecuación cartesiana canónica de una hipérbola con centro de simetría C(0,0), y con eje focal OX,
que es lo que tienes representado en esta opción, por lo que puedes concluir que la opción señalada A si es posible.
B)
Observa que la recta tiene pendiente negativa y distinta de cero, y ordenada al origen positiva y distinta de cero, por lo que puedes plantear (observa que aplicamos propiedades de la función valor absoluto):
b = -|b| y a = |a|;
luego, tienes la primera ecuación de tu enunciado:
a*x2 + b*y2 = a*b, sustituyes expresiones en la primera ecuación de tu enunciado, y queda:
|a|*x2 - |b|*y2 = -|a|*|b|, divides en todos los términos por -|a|*|b|, y queda:
-x2/|b| + y2/|a| = 1,
que es la ecuación cartesiana canónica de una hipérbola con centro de simetría C(0,0), y con eje focal OY,
que es lo que tienes representado en esta opción, por lo que puedes concluir que la opción señalada B si es posible.
C)
Observa que la recta tiene pendiente positiva y distinta de cero, y ordenada al origen positiva y distinta de cero, por lo que puedes plantear (observa que aplicamos propiedades de la función valor absoluto):
b = |b| y a = |a|;
luego, tienes la primera ecuación de tu enunciado:
a*x2 + b*y2 = a*b, sustituyes expresiones en la primera ecuación de tu enunciado, y queda:
|a|*x2 + |b|*y2 = |a|*|b|, divides en todos los términos por |a|*|b|, y queda:
x2/|b| + y2/|a| = 1,
que es la ecuación cartesiana canónica de una elipse con centro de simetría C(0,0),
que es lo que tienes representado en esta opción, por lo que puedes concluir que la opción señalada C si es posible.
D)
Observa que la recta tiene pendiente negativa y distinta de cero, y ordenada al origen positiva y distinta de cero, por lo que puedes plantear (observa que aplicamos propiedades de la función valor absoluto):
b = -|b| y a = |a|;
luego, tienes la primera ecuación de tu enunciado:
a*x2 + b*y2 = a*b, sustituyes expresiones en la primera ecuación de tu enunciado, y queda:
|a|*x2 - |b|*y2 = -|a|*|b|, divides en todos los términos por -|a|*|b|, y queda:
-x2/|b| + y2/|a| = 1,
que es la ecuación cartesiana canónica de una hipérbola con centro de simetría C(0,0), y eje focal OY,
que no es lo que tienes representado en esta opción, por lo que puedes concluir que la opción señalada D no es posible.
Espero haberte ayudado.
-


Jose Ramos
el 9/2/20Tu procedimiento es correcto, pero has hecho mal los cálculos. Si sustituyes bien por los valores en el teorema del coseno te saldrá cos B = - 0,175 y B = 100º. Yo en mi solución no tuve en cuenta una cuestión que a veces se produce al aplicar el teorema de los senos y te dí como solución B = 80º (La solución correcta es B = 100º y sale de que sen B = 0,985 provoca que B sea 80º o 100º y en el caso de tu problema la solución es 100º)
Te lo vuelvo a hacer de las dos formas:
-
Ayuda con este ejercicio!!
En el grupo de las permutaciones de 3 elementos un estudiante realiza los dos productos posibles con las permutaciones de a y b, donde
Luego El conjetura que S3 es el menor grupo no abeliano que existe, pues se acuerda que en la unidad anterior se afirma que todos los grupos de orden 4 son conmutativos, su conjetura significa que otro grupo no abeliano, debe tener cardinalidad mayor o igual que la de S3.
- Calcular los mencionados productos de a y b.
- Determine si S3 es abeliano o no y por que?
- Diga si es cierto o no que S3 es el menor grupo no abeliano que existe y por que?


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Agradezco infinitamente tu respuesta José en el ejercicio
Demuestre de dos maneras diferentes que el polinomio p(x)= X2 - 2 es irreductible en Q(x)
Existe la posibilidad de demostrarlo de otra manera? O esa es la única forma José? Gracias de antemano


Antonio Silvio Palmitano
el 8/2/20Puedes demostrar por Reducción al Absurdo.
Supuesto Absurdo: p(x) = x2 - 2 (1) si es reducible en el conjunto Q(x).
Luego, como el polinomio es reducible en el conjunto de los números racionales, entonces su expresión factorizada es:
p(x) = (x - a)*(x - b), con a ∈ Q ∧ b ∈ Q.
Luego, distribuyes la expresión del polinomio, y queda:
p(x) = x2 - a*x - b*x + a*b, extraes factor común (-x) entre los términos lineales, y queda:
p(x) = x2 - (a + b)*x + a*b (2),
que es la expresión desarrollada del polinomio.
Luego, comparas coeficientes entre las expresiones del polinomio señaladas (2) (1), y queda el sistema de ecuaciones:
-(a + b) = 0, de aquí despejas: b = -a (3),
a*b = -2;
luego, sustituyes la expresión señalada (3) en la segunda ecuación, resuelves el coeficiente en el primer miembro, y queda:
-a2 = -2, divides por -1 en ambos miembros, y queda:
a2 = 2, extraes raíz cuadrada en ambos miembros, y tienes dos opciones:
1°)
a = -√(2), que al sustituir en la ecuación señalada (3) conduce a: b = √(2),
lo que contradice el supuesto señalado (1), porque los dos valores que hemos determinado no pertenecen al conjunto de los números racionales;
2°)
a = √(2), que al sustituir en la ecuación señalada (3) conduce a: b = -√(2),
lo que contradice el supuesto señalado (1), porque los dos valores que hemos determinado no pertenecen al conjunto de los números racionales.
Luego, puedes concluir que el polinomio cuya expresión tienes en tu enunciado no admite raíces racionales y, por lo tanto, es irreducible en el conjunto de los números racionales.
Espero haberte ayudado.
-
Hola amigos, necesito de su ayuda con este problema
Demuestre de dos maneras diferentes que el polinomio p(x)= X2 - 2 es irreductible en Q(x)
Como se puede justificar esto? Ayudenme por favor!!
-