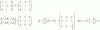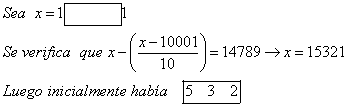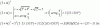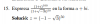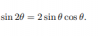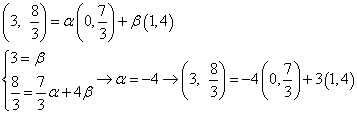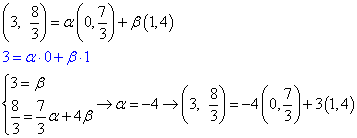-


Breaking Vlad
el 3/2/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
a ver si lo conseguís:
Un hombre va a cobrar un cheque en el que figura una cierta cantidad de euros.Antes de llevarlo al banco se da cuenta de que en la casilla donde se escribe la cantidad hay un poco de espacio delante y detrás del número, y lo aprovecha para escribir la cifra 1 a cada lado. Con este truco recibe 14789€ más de lo que ponía inicialmente en el cheque. Cual era esa cantidad inicial?
-
-
Escribir el vector w=(3, 8/3) como combinación lineal de los vectores u=(0,7/3) y v=(1,4)
¿Cómo se hace? Sé que puede parecer una tontería pero me he liado mazo jaja
-
Hola a todos, alguno me podría ayudar con esta ecuación de primer grado, porque la he tratado de hacer de diferentes formas y el resultado no es el mismo gracias de ante mano.