-
Hola, necesito una fotografía o captura de pantalla con el proceso de la siguiente división de polinomios: (6x4-5x3-4x2+8x-8):(2x2-3x+4) Muchas gracias
-
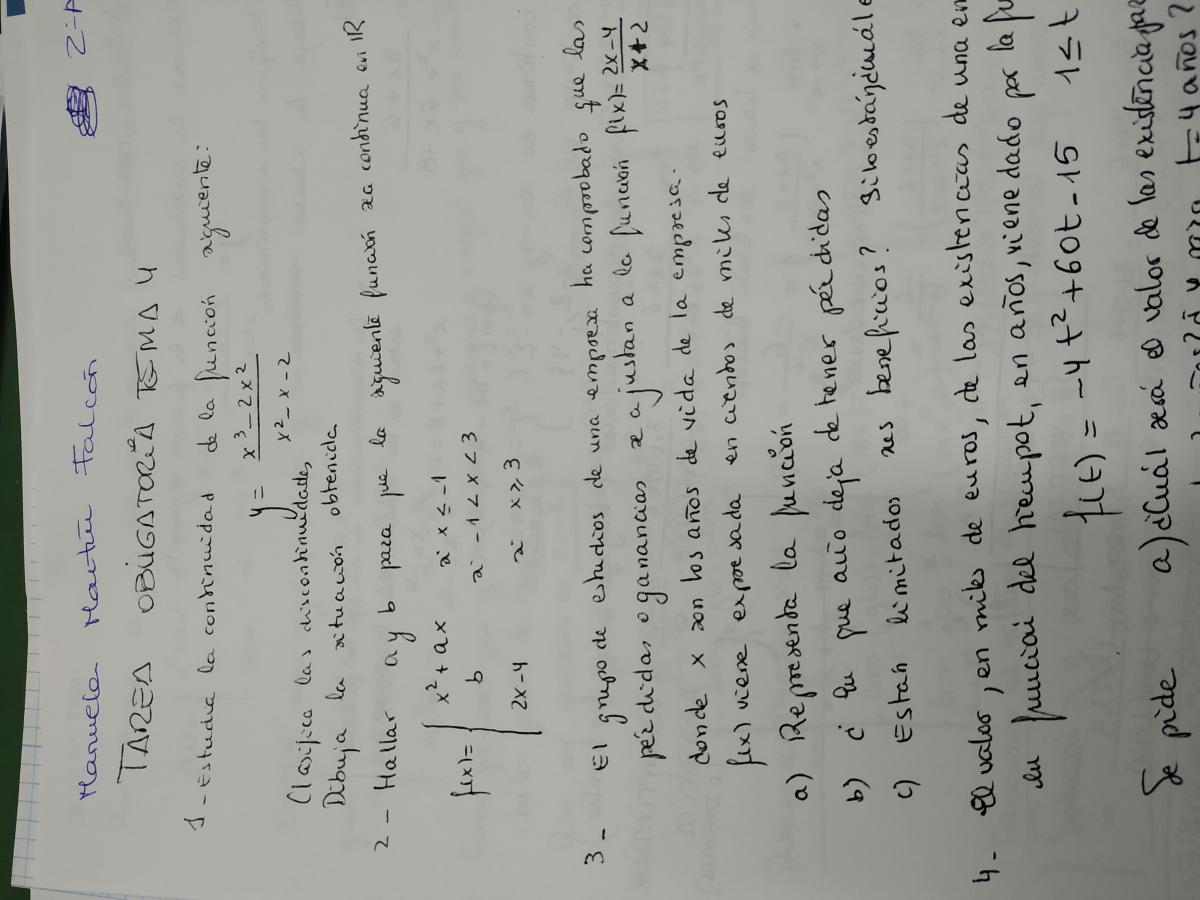 Cómo se resuelve las funciones elementales con fracción, cuando su denominador en de 2ºgrado
Cómo se resuelve las funciones elementales con fracción, cuando su denominador en de 2ºgradoEl ejercicio 1 de la foto


Antonio Silvio Palmitano
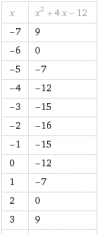
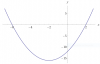
el 29/1/20Tienes la expresión de la gráfica de la función:
y = (x3 - 2*x2) / (x2 - x -2),
factorizas el numerador (observa que puedes extraer factor común: x2), factorizas el denominador (observa que es una expresión polinómica cuadrática mónica, cuyas raíces son: -1 y 2), y queda:
y = x2*(x - 2) / [(x + 1)*(x - 2)] (1),
y observa que el dominio de la función queda expresado, como indica el colega Antonio: D = R - {-1,2} = (-∞;-1) ∪ (-1;2) ∪ (2;+∞).
Luego, una vez establecido el dominio, simplificas la expresión de la gráfica de la función, y queda:
y = x2 / (x + 1).
Luego, tienes dos valores notables para estudiar, que corresponden a las dos "interrupciones" que tienes en tu dominio, para los cuáles aplicas la definición de continuidad de una función en un punto, y queda::
a)
para x = -1 tienes:
1°)
la función no está definida para este valor notable,
2°)
Lím(x→-1-) [x2 / (x + 1) ] = -∞ (observa que el numerador tiende a 1, y que el denominador tiende a cero desde valores negativos),
Lím(x→-1+) [x2 / (x + 1) ] = +∞ (observa que el numerador tiende a 1, y que el denominador tiende a cero desde valores positivos),
por lo que tienes que la función no tiene límite para x tendiendo a -1,
3°)
f es discontinua inevitable en el valor notable: x = -1, y su gráfica presenta Asíntota Vertical, cuya ecuación cartesiana es: x = -1;
b)
para x = 2 tienes:
1°)
la función no está definida para este valor notable,
2°)
Lím(x→2) [x2 / (x + 1) ] = 4/3 (observa que el numerador tiende a 4, y que el denominador tiende a 3),
3°)
f es discontinua evitable en el valor notable: x = -1, y su gráfica presenta discontinuidad puntual, para el valor notable x = -1.
Espero haberte ayudado.
-
Hola! Alguien me podría ayudar con este ejercicio por favor.
Escribe, en forma explícita, la ecuación de la recta que corta al eje de abscisas en el punto x=-2, y cuyo vector director es ⃗v=(1,√3) . ¿Qué angulo forma con el eje de abscisas?

David
el 28/1/20Sacamos la pendiente, que vale: m=√3/1=√3
Ecuación explícita: y=mx+n, con m la pendiente, y n el corte con el eje oy.
Como sabemos el corte con el eje ox y la pendiente, tomamos la ecuación y=mx+n, y sustituimos x e y:
x=-2, y=0 ; 0=√3*(-2)+n ; n=2√3
Ya tenemos la ecuación explícita de la recta: y=√3x+2√3.
El apartado del ángulo lo dejo para que lo pienses y/o alguien pueda colaborar.
-
Buenas alguien me puede ayudar con este ejercicio?
Es el siguiente subconjunto un subespacio vectorial de P2[x]? Justicalo.