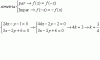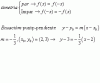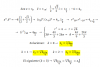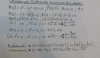-

gonzalezlbl
el 28/1/20La ecuación de la recta viene dada por
y - yo = m (x - xo) donde m es la pendiente de la recta y (xo ; yo) es un punto de la recta.
En este caso m = - 1/3 y (xo ; yo) = (2 ; 3)
Así, la ecuación de la recta es: y - 3 = - ⅓ (x - 2) → y = - ⅓ x + ⅓ • 2 + 3 → y = - ⅓ x + ⅓ • 2 + 3 → y = - ⅓ x + 11/3
-

gonzalezlbl
el 28/1/20Sea L1 la recta 2k x - y - 1 = 0 ; L1 : 2k x - y - 1 = 0 → L1 : y = 2k x - 1 ; así, la pendiente de L1 es m1 = 2k
Sea L2 la recta 3x - 2y - 6 = 0 ; L2 : 3x - 2y - 6 = 0 → L2 : y = (3/2) x - 3 ; así, la pendiente de L2 es m2 = 3/2
Como L1 y L2 son paralelas, se cumple que m1 = m2 → 2k = 3/2 → k = ¾
-
Es posible hacer esta integral sin hacerla por partes o sustitucion? Si es asi ponganme la formula porfa
∫(ln(x))/(2x)


Antonius Benedictus
el 28/1/20El factor contante (1/2) lo sacas fuera multiplicando.
Dentro te queda (1/x)·ln(x)
La estructura de esta expresión es u'·u
Entonces, si pones u'·2u es la derivada de u^2.
Para ello, multiplicas afuera por otro (1/2) y dentro por 2. Y te queda:
(1/4)·∫(1/x)·2 ln (x) dx=(1/4)· (ln (x))^2+C=((ln(x))/2)^2 +C
-


Juan David Rodríguez González
el 28/1/20Comprendo, tiene que dar grado 8 es cierto, pero mi pregunta ese, bajo que regla sale ese factor? es decir, en la teoria tenia entendido que un polinomio factorizado , era todas sus raíces en la forma de (x-a) por el consciente sobrante, en esté caso, (x2 +2) , pero no veo apartir de ahi de donde sacar el ( x2 + √3 ).