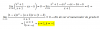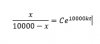-
Laura Muñoz Fernandez
el 1/4/17-Estudia la continuidad de la siguiente función:
x2-k si x∠1
f(x)
kx si x≥1
He resuelto los limites laterales y me da que debo obligar a que k sea =0 ¿Sería correcto?
-
Francisco Marin
el 1/4/17x+3y=0
2x+3y=-5
me salen y=1 y x=-3
seria correcto?la y no me resuelve mucho
gracias
Francisco Marin
el 1/4/17Francisco Marin
el 1/4/17 -
Ingrid
el 1/4/17Me podrían ayudar con este ejercicio, gracias.
Antonio
el 1/4/17 -
Nico
el 1/4/17hola buenas noches, me podrían ayudar con el apartado 2? No puedo con el..
Usuario eliminado
el 1/4/17
Nico
el 1/4/17 -
Juan
el 1/4/17Necesito ayuda con este ejercicio, no tengo ningún otro de referencia y creo que voy mal encaminado:
Es un ejercicio de probabilidad donde tenemos un examen donde participan160 alumnos de 3 institutos (A, B y C) de los cuales analizamos el porcentaje de aprobados (90%, 92% y 83% respectivamente.
b) Probabilidad de que un estudiante al azar no apruebe el examen, he sumado las diferentes ramas y me ha dado 0,135625 (no se si es correcto)
c) Probabilidad de que un estudiante no apruebe y sea del instituto B, calculando la probabilidad condicionada me ha dado 24/217 (no se si es correcto)
d) Probabilidad de que un estudiante no apruebe y no sea del instituto B
e) Sabiendo que el estudiante ha aprobado, que probabilidad hay de que sea del instituto B
A ver si alguien me puede echar una mano con algún apartado, estoy muy perdido...
-
Fermat
el 31/3/17Necesito ayuda con estos dos ejercicios, más o menos complicados.
-
Guillem De La Calle Vicente
el 31/3/17
Bombardero no furtivo de Euclides Problema:
Este es un pequeño acertijo divertido que esperaba compartir con todos ustedes ya que no puedo parecer que lo rompa. Hablé con mi amigo el otro día y él mencionó que los EEUU son capaces de bombardear cualquier punto en la tierra en por lo menos 22 minutos. Calculó que la velocidad de estos bombarderos era de unas 5.000 millas por hora. Si estas cifras son verdaderas o realistas es un tanto irrelevante para mí, cualesquiera que sean los números verdaderos, me convertí en curioso en cómo usted iría sobre calcular el número lo más pequeño posible de planos posible satisfacer estas condiciones.
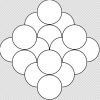
Suponiendo que no estamos tomando en cuenta el despegue, el aterrizaje u otros factores, cada avión sería capaz de volar en cualquier lugar dentro de un círculo de 1833.33 millas de radio en ese período de tiempo. A continuación se muestra una imagen de lo que creo sería la manera más eficiente de distribuir esas áreas (los planos que están en el centro de cada círculo), de modo que todos los puntos pueden ser atravesados.
Ahora si Kyrie Irving y Shaq estaban en lo correcto y el mundo fuera un plano plano 2d, creo que la respuesta sería bastante trivial desde aquí ... circunscribir el patrón en la imagen de arriba dentro de sus límites ... pero siendo que la tierra es un Esfera, digamos una esfera perfecta con una circunferencia de 24,901 millas, - No estoy seguro de cómo abordar esto. No he pensado mucho en la geometría no euclidiana desde la escuela secundaria, y no estoy seguro de cómo lo que recuerdo podría aplicarse.
¡Gracias! Interesado en escuchar sus ideas!
Ángel
el 31/3/17Lo leí hace poco, para que te sigas empapando del tema: http://elpais.com/elpais/2016/08/05/el_aleph/1470398116_486699.html
Guillem De La Calle Vicente
el 31/3/17Intentaré dar una respuesta a mi misma pregunta:
Con una velocidad más realista para los aviones el mundo es plano, o bien podría ser. Una velocidad más realista para los bombarderos es de 1000 mph, lo cual es casi correcto para el bombardero supersónico B-58 estadounidense.
Eso da una distancia de solamente 367 millas en 22 minutos. La curva de la tierra no será importante, así que sólo figura el área de π367² ≈ 423,000 millas cuadradas por plano comparado con una superficie de tierra de π24901² y multiplicar por 4/3 para la superposición de los círculos, dando que se necesita 6138 aviones para cubrir.
Ángel
el 31/3/17Opino que es más práctico considerar los vuelos de los aviones como "planos", pues se podrían considerar los desplazamientos efectuados por los aviones comparados con la superficie total a cubrir de la Tierra casi "infinitésimos, tangenciales y rectos"
Una vez lo interpretas de esta manera, tienes tu modelización (no sabría decirte si acertada o no, con "radio de cobertura" esférica). ¿Quizás modelizarlo con triángulos esféricos serían más realistas? Puede ser...
¿que se complicarían los cálculos o directamente no se podría hacer un cálculo 100% fidedigno? Casi seguro
Guillem De La Calle Vicente
el 1/4/17Maths: esto es bastante preciso, siempre y cuando el radio de los círculos sea pequeño comparado con el radio de la esfera. Estoy considerando la tierra localmente plana y calculando el área cubierta por un círculo de radio la distancia del recorrido. Mi factor 4/3 es para la superposición de círculos en un paquete hexagonal cercano y podría mejorarse un poco. El siguiente nivel de mejora es tratar cada círculo como un casquete esférico y calcular el área sobre esa base. Finalmente usted consigue en los efectos del embalaje que puede ser absolutamente complicado.
Ángel
el 1/4/17¿Has pensado en incorporar grafos en tus círculos acoplados en forma de panal y con ellos hacer caminos de longitud mínima? ¿Sabes utilizar el software maxima?
Es buena idea eso de tomar los desplazamientos de los aviones como celdas de panales de abejas, puedes observar como pueden tomar casi cualquier forma, adaptandose a árboles o techos de las casas....por extensión podrían cubrir la "casi esfera terrestre" por completo y formar un gran esfera (la Tierra o modelizando: la esfera que resulta de los sumatorios de todas las celdas o paquetes de grafos)
Guillem De La Calle Vicente
el 1/4/17Guillem De La Calle Vicente
el 1/4/17 -
Osmaynis Derken González
el 31/3/17 -
Iswag Newton
el 31/3/17
