-
Hallar todos los z pertenecientes a los complejos tal que i^5 por z conjugado^6=81 por z^2, y Im (Z) mayor o igual a cero.use el teorema de moivre,pero no estoy seguro,preciso resolucion, desde Ya gracias.
-


Breaking Vlad
el 27/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola Unicoos ,por favor ayudenme con este ejercicio. No entiendo porqué te dan de dato que la probabilidad de obtener cada número es proporcional al cuadrado del valor .
-
Hola, alguien me podría decir como calcular la convergencia de esta serie?? (-1)^n [n((1+1/n)^2n - (1+2/n)^n)]^ -log(n) . Muchas gracias


Breaking Vlad
el 27/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-







 Buenas tardes Jose, gracias por tu post.
Buenas tardes Jose, gracias por tu post.















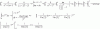








 ¿Me podrían ayudar con el problema 24? Gracias.
¿Me podrían ayudar con el problema 24? Gracias.