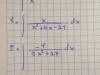logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • Usuario eliminado
    el 18/1/17

    Necesito ayuda con este ejercicio, no consigo sacarlo...

    Me dice que determine a y b sabiendo que el polinomio x3+ax2-2x+b es divisible por x+1 y x-2

    reply•thumb_up•0 voto/s•flag
    icon

    Álvaro Reverte
    el 18/1/17

    Hola Judit.

    Para resolver este ejercicio tienes que echar mano del Teorema del Resto, que dice que al dividir un polinomio P(x) entre un binomio (x - r), el resto de dicha división es el valor numérico del polinomio en "r", es de cir, P(r). En este caso, como queremos que sean divisible queremos que la división sea exacta, por lo que usaremos un caso particular de este teorema que es el Teorema del Factor, el cual dice que un polinomio P(x) es divisible entre un binomio (x - r) si P(r) = 0, es decir su resto se anula. Al preguntarte por dos valores "a" y "b" tendrás que aplicarlo dos veces para poder obtener un sistema y resolverlo.

    Aquí te dejo un vídeo de UNICOOS con un ejemplo algo más sencillo, donde se aplica una sola vez.

    Espero haberte ayudado.

    SB!!

    Teorema del resto Teorema del resto

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    suficiente

  • Usuario eliminado
    el 18/1/17

    Necesito ayuda

    El ejercito me dice que encuentre un polinomio de grado 4 que verifique las siguientes condiciones:

    a) es divisible por x-1

    b)no tiene termino x3

    c)su coeficiente principal es 1

    d)el residuo de la decisión por x-2 vale 15


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/1/17


    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Álvaro Reverte
    el 18/1/17

    Hola de nuevo Judit.

    En este caso te están mandando calcular un polinomio del tipo... P(x) = x4 + ax2 + bx + c, usando las condiciones b) y c). El "problema" es que nos quedan dos condiciones más por usar, la a) y la d), habiendo tres valores que adivinar, por lo que nos saldrían infinitas soluciones distintas, salvo que se te haya olvidado dar algún dato más del ejercicio. De todos modos el enunciado dice que encuentres un polinomio, por lo que podrías fijar una de los tres valores desconocidos a tu parecer y calcular los otros en función al tuyo.

    ¿Cómo aplicar las condiciones que quedan a) y d)? Pues usando lo explicado en la duda anterior.

    Un saludo.

    SB!! 

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Fire Sword99
    el 18/1/17

    Buenas me podrían ayudar con estas dos  integrales racionales con fracción por favor ?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/1/17


    thumb_up•2 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Axel Morales Piñón.
    el 18/1/17

    Perdona el pequeño lapsus amigo Antonio :-) 


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    José Carlos Castillo
    el 18/1/17

    Hola, alguien sabe como podría resolver este determinante usando solamente propiedades de los determinantes?


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/1/17

    A ver si esto te da una idea, José Carlos:


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Paula
    el 18/1/17

    Ayuda con estos ejercicios. Paso a paso, si puede ser.

    Resuelve los siguientes sistemas de ecuaciones:

    a) 2/x+3/y-6/xy=1, x+y=5

    b) x2+xy+y2=21, x+y=1

    c) √x-√y-x=2, 5x=4y


    P.D. ¿Se pueden hacer por cambio de variable? He visto un vídeo de internet que resuelve un sistema no lineal así.


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/1/17

    Paula, intenta hacer el b) poniendo en la 1ª ecuación y=1-x


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Paula
    el 18/1/17

    Muchas Gracias Antonio. Lo intentaré.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Matías Ignacio Loyola Galdames
    el 18/1/17

    No había entendido el a) y el c) ahora vi que los hicieron. Aquí el b) por si acaso.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Paula
    el 18/1/17

    Te lo agradezco Matías Ignacio.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Pablo
    el 18/1/17

    No entiendo este sistema de ecuación no lineal, si alguien puede explicármelo lo agradecería:

    x2 + y2 + xy = 3/4

    x - y2- xy = -1/4

     


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/1/17

    Pablo, pon foto del enunciado original o comprueba si está bien copiado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Antonio Silvio Palmitano
    el 18/1/17

    Recuerda que en un sistema de ecuaciones como el de tu enunciado se puede mantener una de las ecuaciones (por ejemplo la segunda), y reemplazar a la otra (por ejemplo la primera) por la suma de las dos ecuaciones. Hacemos todo y el sistema queda:

    x2 + x = 1/2,

    x -y2 - xy = -1/4.

    Luego, multiplicamos por 2 en todos los términos de la primera ecuación y queda:

    2x2 + 2x = 1, caemos pasaje de término y queda:

    2x2 + 2x - 1 = 0, que es una ecuación poliinómica cuadrática cuyas soluciones son:

    1) x = ( -2 - √(12) )/4 ≅ -1,3660,

    2) x = ( -2 + √(12) )/4 ≅ 0,3660.

    Luego, tenemos opciones para cada caso:

    1) Reemplazamos en la segunda ecuación (empleamos los valores aproximados) y queda:

    -1,3660 - y2 - (-1,3660)*y = -1/4, hacemos pasaje de término, reducimos términos semejantes y queda:

    - y2  + 1,3660*y - 1,1160 = 0, multiplicamos en todos los términos de la ecuación por -1 y queda:

    y2  - 1,3660*y + 1,1160 = 0, que es una ecuación polinómica cuadrática que no tiene soluciones reales;

    2) Reemplazamos en la segunda ecuación (empleamos los valores aproximados) y queda:

    0,3660 - y2 - 0,3660*y = -1/4, hacemos pasaje de término, reducimos términos semejantes y queda:

    - y2 - 0,3660*y + 0,6160 = 0, multiplicamos en todos los términos de la ecuación por -1 y queda:

    y2 + 0,3660*y - 0,6160 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

    2a) y ≅ 0,6229, 

    2b) y ≅ -0,9889.

    Por lo tanto, tenemos que el conjunto solución (con valores aproximados) queda: S = { (0,3660 , 0,6229) , (0,3660 , -0,9889) }.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Guillem De La Calle Vicente
    el 18/1/17


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/1/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Pablo
    el 18/1/17

    Una pregunta, ¿no hay video de sistemas de inecuaciones de una incógnita? Si así es, no lo encuentro y me gustaría que me pasarais un enlace ya que he visto que solo hay videos con una incógnita. Gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Matías Ignacio Loyola Galdames
    el 18/1/17

    Más arriba puedes usar el buscador de unicoos.

    http://www.unicoos.com/buscar?nombre=inecuaciones

    Ahí salen.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Guillem De La Calle Vicente
    el 18/1/17

    Define el concepto de función derivable en un punto xo.


    reply•thumb_up•0 voto/s•flag
    icon

    Silvia
    el 18/1/17

    Una función es derivable en un punto x=a si existe el límite de esa función

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Antonio Silvio Palmitano
    el 18/1/17

    Definimos a la derivada de una función de una variable con expresión f(x) en un punto x0 perteneciente a su dominio en estas dos foramas:

    f ' (x0) = Lím(h→0) ( f(x0+h) - f(x0) ) / h,

    f ' (x0) = Lím(x→x0) ( f(x) - f(x0) ) / (x - x0),

    las dos maneras son equivalentes.

    Recuerda que gráficamente, la derivada de una función evaluada en uno de los puntos de su dominio es igual a la pendiente de la recta tangente a la gráfica de la función, que pasa por el punto de coordenadas: P0( x0 , f(x0) ).

    Espero haberte ayudado.



    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Elia
    el 18/1/17

    como se resuelve?

     encuentra la recta paralela a 2x+3y+1=0 con ordenada en el origen=2


    reply•thumb_up•0 voto/s•flag
    icon

    Matías Ignacio Loyola Galdames
    el 18/1/17

    Ojalá te sirva. Saludos.



    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo