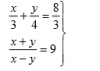Imposible leer la foto que adjuntaste.

Intento de nuevo. Gracias

Primero que todo, observa que x debe ser distinto de y, para que no se indetermine la segunda ecuación.

Luego, multiplicas por 12 en todos los términos de la primera ecuación, haces pasaje de divisor como factor en la segunda y queda:

4x + 3y = 32

x + y = 9(x - y),

distribuyes, haces pasaje de términos en la segunda ecuación y queda:

 4x + 3y = 32

-8x + 10y = 0,

luego, puedes despejar en la segunda ecuación y queda: y = 8x/10 = (4/5)x (*),

luego sustituyes en la primera ecuación y queda:

4x + (12/5)x = 32, multiplicas en todos los términos por 5 y queda:

20x + 12x = 160, reduces términos semejantes y queda:

32x = 160, de donde puedes despejar x = 5;

luego sustituyes en la expresión señalada (*) y tienes: 

y = (4/5)*5, resuelves y queda: y = 4.

Observa que la solución: x = 5, y = 4 es válida, ya que no indetermina a la segunda ecuación del sistems inicial.

Espero haberte ayudado.

Me falta algo, el numero de pasajeros en cada ruta.. ¿es ese el enunciado completo y lliteral?

Aplica Vietta, la formula de toda la vida... En este caso c=a..... [-b±√(b² -4.a.a)]/(2a)... 
Si b²-4a²=0 tendrás una raiz doble igual a -b/(2a)
Si b²-4a²>0 tendrá dos raices
Si b²-4a<0 no tendrá solución. 
A partir del enunciado no podemos asegurar nada más..

Si lo acompañas al menos de un dibujo...

Buscas:  1*2*3*...*(n-2)*(n-1)*n = n!.

Luego, debes encontrar un producto de n factores, en los cuáles al descomponer en factores primos obtengas veintinueve veces a 2 como factor (descomponemos solamente los factores pares):

1* 2*3*(2²)*5*(2*3)*7*(2³)*9*(2*5)*11*(2²*3)*13*(2*7)*15*(2⁴)*17*(2*9)*19*(2²*5)*21*(2*11)*23*(2³*3)*25*

*(2*13)*27*(2²*7)*29*(2*15)*31*(2⁵) = 32!

Observa que si sumas los expoenentes de 2 de todos los factores, queda 31, por lo que 2³¹ = 2²*2²⁹ es factor de 32!.

Por lo tanto, tenemos que el mínimo factorial múltiplo de 2²⁹ es 32!.

Espero haberte ayudado.

Se supone una extracción simultánea (sin orden ni reposición).

Casos posibles C(2n+1,2)=(2n+1)·2n/2=n(2n+1)

Casos favorables  (bola impar y bola par):  C(n+1,1)·C(n,1)=(n+1)·n

Probabilidad pedida:

(n+1)/(2n+1)

Planteamos la ecuación vectorial paramétrica para la recta que pasa por el punto Po(1,-1,3) y tiene vector director v = <2,1,-2>:

<x,y,z> = <1,-1,3> + t<2,1,-2>, con t ∈ R

resolvemos las operaciones en el segundo miembro y queda:

<x , y , z> = <1+2t , -1 + t , 3 - 2t >, luego igualamos componente a componente y queda el sistema de ecuaciones cartesianas paramétricas de la recta:

x = 1+2t

y = -1 + t

z = 3 - 2t 

con t ∈ R

Luego, vamos a investigar si el punto P₁(3,03) pertenece a la recta. Para ello, reemplazamos sus coordenadas en las ecuaciones, y queda el sistema:

3 = 1+2t

0 = -1 + t

3 = 3 - 2t

Observa que tenemos un sistema de tres ecuaciones con una incógnita, por lo que resolvemos con una ecuación y verificamos en las otras dos: si verifican, tenemos que el punto pertenece a la recta, y si una o ambas no verifican, tenemos que el punto no pertenece a la recta.

De la tercera ecuación podemos despejar: t = 0,

y al reemplazar en la primera ecuación queda:

3 = 1 + 2*0 = 1, que es una identidad absurda, por lo que tenemos que el punto P₁ no pertenece a la recta.

En forma similar, puedes proceder con los demás puntos.

Espero haberte ayudado.

Por favor, envía el enunciado de tu ejercicio para que podamos ayudarte