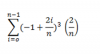-
Buenas noches.Una consulta, tengo este sistema:
x+y-z=1
3x+2y+z=1
5x+3y+4z=2
-2x-y+5z=6
Necesito analizarlo. Queria saber si se puede calcular el rango tanto de la matriz de los cofactores como la de la ampliada mediante determinantes. Porque en el libro, la solucion es que el sistema es indeterminado rgo(A)=2 y rgo(ampliada)=4.Pero yo lo hago por determinantes y me sale que tienen rango 3. Como deberia calcularlo?
-
hola a todos, los molesto con una integral...
∫ln (x/x+1)


Antonio Silvio Palmitano
el 21/11/16Puedes aplicar la propiedad del logaritmo de una división:
ln( x/(x+1) ) = lnx - ln(x+1),
luego sustituyes y la integral queda:
I = ∫ ln ( x/(x+1) )dx = ∫ ( lnx - ln(x+1) )dx,
separas en términos y queda:
I = ∫ lnx dx - ∫ ln(x+1)dx.(*)
Luego, observa que puedes resolver las dos integrales con el método de integración por partes
a) en la primera planteamos:
u = lnx, de donde tienes: du = dx/x,
dv = 1dx, de donde tienes: v = x,
luego pasamos a la integral:
∫ lnx dx = xlnx - ∫ x dx/x = xlnx - ∫ 1dx = xlnx - x + C; (**)
b) en la segunda integral planteamos:
u = ln(x+1), de donde tienes: du = dx/(x+1),
dv = dx, de donde tienes: v = x,
luego pasamos a la integral:
∫ ln(x+1) dx = xln(x+1) - ∫ x dx/(x+1) = xln(x+1) - ∫ ( 1 - 1/(x+1) )dx = xln(x+1) - x - ln(x+1) + C. (***)
Por último, sustituimos las expresiones señaladas (**) (***) en la expesión señalada (*) y queda:
I = ∫ lnx dx - ∫ ln(x+1)dx = xlnx - x - ( xln(x+1) - x - ln(x+1) ) + C = xlnx - x - xln(x+1) + x + ln(x+1) ) + C,
cancelamos términos opuestos y llegamos a:
I = xlnx - xln(x+1) + ln(x+1) ) + C.
Espero haberte ayudado.
-
Hola.
Por favor podrían ayudarme con estas integrales:
De antemano gracias
- ∫(x^3+x-1)/((x^2+1)^2) dx
- ∫1/((x^2+1)^2) dx


Antonio Silvio Palmitano
el 21/11/16Vamos con una orientación: en los dos ejercicios debes plantear fracciones parciales, y observa que el denonimandor tiene un factor doble de segundo grado.
a) Planteamos:
(x3+x-1)/(x2+1)2 = (ax + b)/(x2+1) + (cx + d)/(x2+1)2 = extraemos denominador común:
= ( (ax + b)(x2+1) + cx + d )/(x2+1)2 , luego comparamos numeradores y queda la igualdad entre polinomios:
(ax + b)(x2+1) + cx + d = x3 + x - 1
Luego, como tenemos cuatro coeficientes para determinar, evaluamos para cuatro valores arbitrarios, por ejemplo: x = 0, 1, -1, 2, y queda el sistema de ecuaciones:
b + d = -1
2(a + b) + c + d = 1
2(-a + b) - c + d = -3
5(2a + b) + 2c + d = 9
Luego, queda para que resuelvas el sistema y continúes la tarea.
b) El planteo es el mismo, lo haces y llegarás a la igualdad entre polinomios:
(ax + b)(x2+1) + cx + d = 1
Luego, evalúas para los mismos valores de x del ejercicio anterior, y queda el sistema de ecuaciones:
b + d = 1
2(a + b) + c + d = 1
2(-a + b) - c + d = 1
5(2a + b) + 2c + d = 1.
Haz el intento de terminar el trabajo, y si te es necesario puedes volver a consultar.
Espero haberte ayudado.
-
ayuda con esta integral
∫1+2cos2θdθ


Antonio Silvio Palmitano
el 21/11/16Puedes comenzar por separar en términos, y extraer factor constante en el segundo término, y la integral queda:
I = ∫ 1dθ + 2 ∫ cos(2θ)dθ = θ + sen(2θ) + C.
Observa que la integral para el segundo miembro puedes resolverla con la sustitución:
w = 2θ, de donde tienes: dw = 2dθ, y luego tienes: dw/2 = dθ, luego sustituyes y el segundo término queda:
2 ∫ cos(2θ)dθ = 2 ∫ cos(w)dw/2 = 2(1/2) ∫ cos(w)dw = 1sen(w) + C = sen(2θ) + C.
Espero haberte ayudado.
-
Buenas noches.Tengo una pregunta con respecto a planos. Si me dan 3 puntos, y me piden:
1) Hallar ecuacion del plano que pasa por dichos puntos
Me dan otros 3 puntos y me piden:
1)Hallar ecuacion del plano que contiene a dichos puntos
Yo lo resuelvo al primero haciendo determinante 3x3, con dos vectores calculados de los puntos dados. Es el mismo procedimiento en ambos enunciados? o es distinto que pase a que lo contenga?
-
Hola,
Por favor su ayuda con esta derivada implícita.
sen(x) + 2cos(2y)=1
Mil gracias!!


Antonio Silvio Palmitano
el 21/11/16Derivamos término a término con respecto a x (observa que en el segundo término del primer miembro debemos aplicar la regla de la cadena):
cos(x) - 2sen(2y)*2y ' = 0, hacemos pasaje de término, resolvemos coeficientes en el primer miembro y queda:
- 4sen(2y)*y ' = - cos(x), hacemos pasaje de factor como divisor y queda:
y ' = cos(x) / 4sen(2y), con la condición: 4sen(2y) ≠ 0.
Espero haberte ayudado.
-
No se si corresponde para este foro, pero me aparecio en un ejercicio en el temas de integrales, creo que es de Suma de Riemann, si alguien me puede dar una mano ..


Antonio Silvio Palmitano
el 21/11/16Observa que la sumatoria corresponde a la suma inferior para la integral de la función cuya expresión es : f(x) = x3, en el intervalo [-1,1], cuyo resultado es 0.
Luego pasamos a la sumatoria. Si desarrollas el binomio elevado al cubo, queda:
( - 1 + 2i/n )3 = - 1 + 6i/n - 12i2/n2 + 8i3/n3 .
Luego, planteamos el argumento de la sumatoria:
( - 1 + 2i/n )3(2/n) = ( - 1 + 6i/n - 12i2/n2 + 8i3/n3 )(2/n) = - 2/n + 12i/n2 - 24i2/n3 + 16i3/n4.
Luego pasamos a la sumatoria entre 0 y (n-1): separamos en términos, extraemos factores constantes, y queda:
∑( - 1 + 2i/n )3(2/n) = - (2/n)∑1 + (12/n2)∑i - (24/n3)∑i2 + (16/n4)∑i3 =
luego resolvemos sumatorias (puedes probar por inducción completa) y queda:
= - (2/n)(n -1) + (12/n2)(n - 1)n/2 - (24/n3)(n - 1)n(2n - 1)/6 + (16/n4)(n -1)2n2/4 =
simplificamos divisores y factores en cada término:
= - (2/n)(n -1) + (6/n)(n - 1) - (4/n2)(n - 1)(2n - 1) + (4/n2)(n -1)2 =
reducimos los dos primeros términos y extraemos factor común en los dos últimos:
= (4/n)(n - 1) + (4/n2)(n - 1)( - (2n - 1) + n - 1) =
reducimos el último factor en el segundo término:
= (4/n)(n - 1) + (4/n2)(n - 1)(- n) =
distribuimos divisores en cada término y resolvemos el signo en el segundo término:
= 4(1 - 1/n) - 4(1 - 1/n) = 0.
Observa que ahora puedes tomar el límite cuando n tiende a + infinito, y queda:
Lím(n->+inf) ∑( - 1 + 2i/n )3(2/n) =
= Lím(n->+inf) ( 0 ) = 0.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 21/11/16Observa el argumento de la sumatoria:
el factor (2/n) nos da la longitud de un subintervalo, al haber dividido un intervalo de longitud 2 en n partes;
el otro factor, nos indica que el intervalo comienza en x = -1, y se evalúa la función en cada uno de los extremos izquierdos de los subintervalos, los que son:
- 1 + 0*2/n, -1 + 1*2/n, -1 + 2*2/n, -1 + 3*2/n, ..., -1 + (n-1)*2/n, observa que contamos desde 0 hasta (n-1).
Luego, como tenemos en el argumento: (-1 + 2i/n)3, es de aquí de donde concluimos que la función tiene expresión f(x) = x3.
Recuerda que en los argumentos de la sumas de Riemann tenemos productos de la forma: f(xi)*(b - a)/n, para el intervalo [a,b], con xi elemento de cada subintervalo (en este ejercicio que vimos son los extremos izquierdos).
Espero haberte ayudado.
-
Hola unicoos;
He realizado este problema y en las soluciones si me coincide que el resultado DB=√13cm, pero no me coindice en que AD sea 7,5cm .
En la solución pone que AD= 0,83cm.
No sé en qué paso he fallado, me podrían ayudar?


Antonio Silvio Palmitano
el 21/11/16Vamos con una orientación.
Llamemos O al centro de la circunferencia.
Observa que el triángulo COD es isósceles: |CO| = |OD| = 2, y |CD| = √(3). Luego planteamos el Teorema del Coseno para calcular la medida del ángulo α, correspondiente al vértice O:
|CD|2 = |C0|2 + |OD|2 - 2|CO||OD|cosα, reemplazamos, resolvemos términos y queda:
3 = 4 + 4 - 8cosα, de donde podemos despejar:
cosα = 5/8, que corresponde al ángulo cuya medida es: α ≅ 51,32°.
Luego, si llamamos β al ángulo con vértice B en el triángulo CBA, y si llamamos γ al ángulo con vértice C en el triángulo DCA, tenemos:
α es un ángulo central, β es un ángulo inscripto, y γ es un ángulo semiinscripto en la circunferencia, por lo que tenemos para sus medidas:
"el ángulo inscripto mide la mitad del ángulo central correspondiente": β = α/2 ≅ 25,66°;
Haz el intento de continuar a partir de aquí, y si te es necesario, puedes volver a consultar.
Espero haberte ayudado.
"el ángulo semiinscripto mide la mitad del ángulo central correspondiente": γ = α/2 ≅ 25,66°;
luego haz el intento de continuar a partir de aquí y, si te es preciso, puedes volver a consultar.
Espero haberte ayudado.
-
Hola, necesito que me corroboren si estoy bien en esta derivada implicita, 4x^2y-3y= x^3-1 mi resultado es y'= 3x^2/8x-3, ayuda por favor.


Antonio Silvio Palmitano
el 20/11/16Si la ecuación es: 4x2y - 3y = x3 - 1, derivamos término a término y queda:
8xy + 4x2y ' - 3y ' = 3x2, hacemos pasaje de término y queda:
4x2y ' - 3y ' = 3x2 - 8xy, extraemos factor común en el primer miembro y queda:
y ' (4x2 - 3) = 3x2 - 8xy, hacemos pasaje de factor como divisor y llegamos a:
y ' = (3x2 - 8xy) / (4x2 - 3), con la condición: 4x2 - 3 ≠ 0.
Espero haberte ayudado.