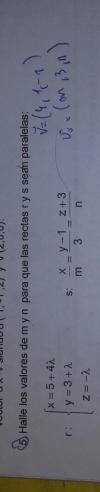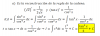-3+0i

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Muchas gracias amigo!

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Es muy posible te ayuden estos vídeos que grabé como excepción... Integrales Impropias

No hay ningun problema y perdon por preguntar cosas que no se hayan visto. Disculpame. Muchas gracias por tus videos David, me ayudan muchisimo en la universidad. 

No es una indeterminación del tipo 1∞, Pepito. La base de la`potencia tiene por límite 4/5  y el exponente tiene por límite 0. El resultado es:

(4/5)⁰=1

Que es lo que te da a ti., solo por casualidad. 

Expresamos al número complejo genérico en forma binómica: z = x + yi, luego, la ecuación queda:

Re( (x + yi)² - 4(x - yi) ) = 0, desarrollamos el argumento en el primer miembro:

Re( x² + 2xyi - y² - 4x + 4yi ) = 0, agrupamos términos reales e imaginarios por separado:

Re( (x² - y² - 4x) + (2xy + 4y)i ) = 0, resolvemos el primer miembro (nos quedamos con la parte real del argumento):

x² - y² - 4x = 0 (observa que la curva es una hipérbola).

Luego derivamos implícitamente con respecto a x:

2x - 2y*y ' - 4 = 0, dividimos por 2 en todos los términos de la ecuación y queda:

x - y*y ' - 2 = 0, despejamos y queda:

(x - 2)/y = y '.

Luego, observa que la expresión se indetermina para el punto de coordenadas: Z(4,0), ya que el numerador toma el valor -2, y el denominador toma el valor 0. Por lo tanto, tenemos que la recta tangente en el punto es paralela al eje coordenado OY, y su ecuación es: x = 4.

Luego, como la recta normal en el punto es perpendicular a la recta tangente, tenemos que la recta normal es paralela el eje coordenado OX, y su ecuación es y = 0 (observa que la recta normal coincide con el eje OX).

Espero haberte ayudado.

Consideremos, para los incisos (a) y (b) la sucesión cuyo elemento general es: b_n = sen(n), y observa que está acotada, ya que: - 1 ≤ b_n ≤ 1, para todo n ∈ N.

a) Consideremos la sucesión con elemento general: c_n = 2cos(n), y observa que también está acotada, ya que: - 1 ≤ b_n ≤ 1, para todo n ∈ N.

Luego, tenemos para el elemento general de la sucesión a_n:

a_n = b_n*c_n = sen(n)*2cos(n) = sen(2n), y observa que también está acotada, ya que: - 1 ≤ b_n ≤ 1, para todo n ∈ N. pero no es convergente, ya que sus elementos oscilan entre -1 y 1.

b) Consideremos la sucesión con elemento general constante: c_n = 1, observa que converge a 1.

Luego, tenemos para el elemento general de la sucesión a_n:

a_n = b_n*c_n = sen(n)*1 = sen(n), y observa que también está acotada, ya que: - 1 ≤ b_n ≤ 1, para todo n ∈ N. pero no es convergente, ya que sus elementos oscilan entre -1 y 1.

c) Observa que tienes que 1/c_n tiende a infinito, por lo que sabemos entonces que c_n tiende a 0.

En este caso, el elemento general de la sucesión a_n:

a_n = b_n*c_n tiende a 0, y la sucesión resulta convergente en este caso. Para visualizarlo, planteamos el límite, y consideramos que la sucesión b_n está acotada entre L₁ y L₂, con L₁ y L₂ números reales (consideramos que |L₁| ≤ |L₂|:

| Lím(n->+inf) a_n | = | Lím(n->+inf) b_n*c_n | = | Lím(n->+inf) b_n * Lím(n->+inf) c_n | =

= | Lím(n->+inf) b_n | * | Lím(n->+inf) c_n | ≤ |L₂| * 0 = 0.

Luego, concluimos que las afirmaciones (a) y (b) son falsas, y que la afirmación (c) es verdadera.

Espero haberte ayudado.