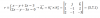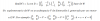-
Tengo dudas con planos y rectas. Si me piden un plano, que pasa por un punto y es perpendicular a la recta interseccion de dos planos..digamos..
R: x-y+2z=3
2x-y-3z=0
Tengo entendido que para encontrar el plano, solo necesito calcular su vector normal, y el vector director de esa recta seria el normal del plano por ser perpendicular, bueno la duda esta en como encontrar el director de la recta. Lo hize resolviendo el sistema por reduccion y llego a la ecuacion parametrica, pero nose si lo hice bien.Esto es lo que me salio:
X= t(lambda)
Y=-9/5 + 7/5t
Z=3/5 + 1/5t
Esta bien resuelto? Hay otra manera de encontrar el director?
-
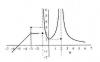
Hola, me pueden ayudar con el siguiente ejercicio de límites? empieza con la gráfica de una función y me piden determinar si existen los siguientes límites:
a) lim cuando x tiende a -1 de f(x)
b) lim cuando x tiende a 2 de f(x)
Debo empezar calculando los límites laterales según lo indicado en la gráfica? no me dan la función, solo esa gráfica.
Hasta ahora me ha dado:
a) no existe ya que cuando nos acercamos por la derecha es igual a +∞ y por la izquierda es igual a 2.
b) no existe ya que cuando nos acercamos tanto por la izquierda como por la derecha tiende a +∞
Son correctos esos resultados?
-


Antonio Silvio Palmitano
el 19/11/16Puedes comenzar por resolver el segundo miembro, y la ecuación queda:
(1/3)log3x = 1/9, luego multiplicas por 3 en ambos miembros, resuelves el segundo miembro y queda:
log3x = 1/3, luego compones en ambos miembros con la función inversa del logaritmo en base 3 y queda:
x = 31/3, luego puedes expresar como raíz y queda:
x = ∛(3).
Espero haberte ayudado.
-
ALGUIEN me aydua con este LIMITE?? llegue a eso despues de calcular el valor de una integral impropia.
Pregunta extra pued juntar los logaritmos que aparece en el limite. como un cociente


Antonio Silvio Palmitano
el 20/11/16Observa que el último término tiende a π/2, ya que el argumento del arco-tangente tiende a + infinito.
Luego, nos quedan para resolver los dos términos logarítmicos, para ello, vamos a extraer factor común en sus argumentos, los tratamos por separadao:
- log(x + 1) = - log( x(1 + 1/x) ) = - ( logx + log(1 + 1/x) ) = - logx - log(1 + 1/x);
(1/2)log(x2 + 4) = (1/2)log( x2(1 + 4/x2) ) = (1/2)( log(x2) + log(1 + 4/x2) ) = (1/2)( 2logx + log(1 + 4/x2) ) = logx + (1/2)log(1 + 4/x2).
Luego, planteamos los dos primeros términos juntos:
- log(x + 1) + (1/2)log(x2 + 4) = - logx - log(1 + 1/x) + logx + (1/2)log(1 + 4/x2) = cancelamos términos opuestos:
= - log(1 + 1/x) + (1/2)log(1 + 4/x2) = aplicamos la propiedad del logaritmo de una division:
= log( (1 + 4/x2) / (1 + 1/x) ).
Luego, la expresión del enunciado podemos escribirla en dos términos:
Lím(x->+inf) log( (1 + 4/x2) / (1 + 1/x) ) + Lím(x->+inf) ( arctan(x/2) ) =
Observa que el argumento del logaritmo tiende a 1, y como ya hemos dicho, el argumento del arco-tangente tiende a + infinito:
= 0 + π/2 = π/2.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 20/11/16Observa que debe cumplirse: logx2 ≠ -1.
Luego, comencemos hacemos pasaje de divisor como factor y queda:
1 + log2x = 1 + logx2, cancelamos términos y queda:
log2x = logx2, luego comparamos argumentos, y comparamos bases y queda:
x = 2, y observa que se cumple la condición que enunciamos al comienzo: log22 = 1 ≠ -1.
Espero haberte ayudado.
-
 Hola, me gustaría que alguien me ayudase con este ejercicio si no es demasiada molestia! Muchas gracias de ante mano :)
Hola, me gustaría que alguien me ayudase con este ejercicio si no es demasiada molestia! Muchas gracias de ante mano :)

Antonio Silvio Palmitano
el 20/11/16Observa que por medio de la división del numerador por el denominador, la expresión de la función puede escribirse.
g(x) = x - x/(x2 + 1) = x - x(x2 + 1)-1, también observa que el dominio de la función es R.
Luego pasamos a plantear la expresión de su derivada primera:
g ' (x) = 1 - (x2 + 1)-1 + 2x2(x2 + 1)-2, observa que está definida para todo R.
Luego pasamos a plantear la expresión de su derivada segunda, que luego de operar queda:
g ' ' (x) = 6x(x2 + 1)-2 - 8x3(x2 + 1)-3, observa que también está definida en todo R.
Luego planteamos la condición de posible punto de inflexión:
g ' ' (x) = 0, sustituimos y queda:
6x(x2 + 1)-2 - 8x3(x2 + 1)-3 = 0, hacemos pasaje de término y queda:
6x(x2 + 1)-2 = 8x3(x2 + 1)-3 , expresamos como fracciones y queda:
6x / (x2 + 1)2 = 8x3 / (x2 + 1)3 , hacemos pasaje de divisor como factor, simplificamos y queda:
6x(x2 + 1) = 8x3 , distribuimos el primer miembro, hacemos pasaje de término y queda:
6x3 + 6x - 8x3 = 0, dividimos en todos los términos de la ecuación por 2, reducimos términos semejantes y queda:
- x3 + 3x = 0, extraemos factor común en el primer miembro y queda:
- x(x2 - 3) = 0, multiplicamos por -1 en ambos miembros, factorizamos el agrupamiento y queda:
x( x - √(3) )( x + √(3) ) = 0, luego por anulación de un producto, tienes en cada factor una raíz:
x = 0
x = √(3)
x = - √(3)
Luego, queda para que estudies el signo de la derivada segunda en los intervalos:
( -inf , - √(3) )
( - √(3) , 0 )
( 0 , √(3) )
( - √(3) , +inf )
tarea que puedes realizar evaluando con un valor representante en cada uno de ellos (te dejo el trabajo para que lo concluyas).
Espero haberte ayudado.
-
Hola, me gustaría que alguien me ayudase con este ejercicio si no es demasiada molestia! Muchas gracias de ante mano :)


Jonathan Sánchez Millones
el 20/11/16Holas, perdonad la mala calidad( es lo mas que puedo hacer :D ya que no tengo escáner ni celular por el momento), espero lo logres entender
Finalmente lo que tienes que hacer es: Los puntos criticos que te hallas resultado en la primera derivada los evaluas en la segunda derivada, si te sale un numero > 0 es porque en un minimo, si te resulta un numeroz < 0 es porque hay un maximo.
Ejemplo:
Si un punto critico de la primera derivada fuese x=1 y evaluado en la funcion original te resulta f(x)= 2 , entonces (1.2) es un posible extremo, y supongamos que x=1 evaluado en la segunda derivada te da cualquier numero(nos importa el signo) negativo(< 0), esto quiere decir que en (1.2) hay un maximo (si lo contrario xD).
PD: Espero haberte ayudado xD , saludos :D.

Jonathan Sánchez Millones
el 20/11/16Holas, lo primero que teneis que hacer es calcular la primera derivada y esta igualarla a 0(f(x)´=0) para obtener los puntos criticos, estos los evaluas en la funcion original f(x)(para obtener y),luego
para comprobar que tu (x,y) es un extremo(maximo o minimo) calculas la segunda derivada y esta la evaluas(el x) en los puntos criticos que te hallas resultado de la primera derivada y si te resulta un numero(cualquiera) > 0 entonces es porque es un minimo, de lo contrario( un numero < 0 ) es porque es un maximo
PD: Recordad que el numero que te resulte de evaluar en la segunda no nos interesa solo su signo para saber si es un maximo o minimo, si te resultase un 0 es por que el criterio de la segunda derivada no decide nada sobre el numero critico x=0, en este caso solo se recurre al criterio de la primera derivada(evaluar en los intervalos el crecimiento y decrecimiento) como bien lo sabes hacer :)
Espero haberte ayudado, saludos :D
-
Hola, me pueden explicar por favor, como resolver este ejercicio por integración de funciones racionales
∫ dx/ (x(x-1)^2)
Muchas gracias


Antonio Silvio Palmitano
el 20/11/16Vamos con una orientación. Observa que el denominador tiene un factor simple y uno doble, ambos de grado 1, por lo que planeamos:
a/x + b/(x-1) + c/(x-1)2 = 1 / x(x-1)2, extraemos denominador común en el primer miembro y queda:
( a(x-1)2 + bx(x-1) + cx ) / x(x-1)2 = 1 / x(x-1)2, comparamos numeradores y queda la igualdad entre polinomos:
a(x-1)2 + bx(x-1) + cx = 1, luego evaluamos en tres valores distintos, por ejemplo 1, 0 y -1, lo hacemos y queda el sistema de ecuaciones:
c = 1
a = 1
4a + 2b - c = 1, de donde tienes: b = -1.
Luego, puedes pasar al cálculo de la integral:
I = ∫ dx/ (x(x-1)2) = ∫ dx/x - ∫ dx/(x-1) + ∫ dx/(x-1)2 , resolvemos y queda:
I = ln|x| + ln|x-1| - 1/(x-1) + C.
Espero haberte ayudado.
-
- Hola, alguien me puede ayudar con las funciones exponenciales? he estado buscando videos pero no encuantro y tengo el trimestral dentro de poco. Graciasss <3