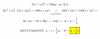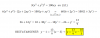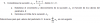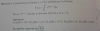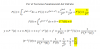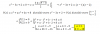-
 Buenas noches, alguien me podría ayudar a resolver estos dos ejercicios porfavor? En el a) tendría que hacer una derivada en implícita ya que tengo dos variables, pero no estoy muy seguro del resultado.
Buenas noches, alguien me podría ayudar a resolver estos dos ejercicios porfavor? En el a) tendría que hacer una derivada en implícita ya que tengo dos variables, pero no estoy muy seguro del resultado.

Antonio Silvio Palmitano
el 17/11/16Vamos con el ejercicio (a). Comencemos por derivar implícitamente (aceptamos que y es función de x en un entorno del punto Po(3,1)):
6(x2 + y2)( 2x + 2yy ' ) = 100y + 100xy ', luego evaluamos para el punto de estudio y queda:
6(9 + 1)( 6 + 2y ' ) = 100 + 300y ', resolvemos factores en el primer miembro y queda:
60( 6 + 2y ' ) = 100 + 300y ', distribuimos en el primer miembro y queda:
360 + 120y ' = 100 + 300y ', dividimos por 20 en todos los términos de la ecuación y queda:
18 + 6y ´= 5 + 15y ', hacemos pasajes de términos, reducimos términos semejantes y queda:
- 9y ' = -13, dividimos por -9 en ambos miembros y queda
y ' = 13/9 = m, donde m es la pendiente de la recta tangente en el punto de estudio.
Luego, a partir de la expresión general de la ecuación cartesiana de una recta, planteamos:
y = (13/9)(x - 3) + 1, que es una forma de la ecuación cartesiana explícita de la recta tangente buscada.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 17/11/16Vamos con el ejercicio (b). Comienza por observar (haz un gráfico) que la semicircunferencia está en el semiplano superior, y que es simétrica con respecto al eje de ordenadas OY, en un sistema cartesiano.
Luego, a partir de un punto cualquiera del primer cuadrante que pertenezca a la semicircunferencia, plantea gráficamente sus coordenadas, te quedan: P(x,y), con y = √(25 - x2).
Luego, observa que tienes un punto simétrico en el segundo cuadrante, que también pertenece a la semicircunferencia, y sus coordenadas son: Q(-x,y), con y = √(25 - x2).
Luego, observa que las dimensiones del rectángulo quedan:
base: b = distancia entre P y Q = 2x.
altura: h = ordenada de P y Q = y.
Luego, el área queda planteada:
A = b*h = xy,
pero como los puntos P y Q pertenecen a la semicircunferencia, sustituimos a partir de la ecuación remarcada y tenemos la función:
A(x) = x√(25 - x2), con 0 < x < 5 (observa que x no puede ser igual a cero ni a cinco).
Luego puedes continuar con el estudio de la función, como has visto con seguridad en clase.
Espero haberte ayudado.
-
Dados los numeros complejos z = -2 + 3i y z1 = -1 + i, hallar otros dos numeros complejos z2 y z3 de
modo que z1, z2 y z3 formen un triangulo equilatero con centro en el numero complejo z.
Gracias de antemano.


Antonio Silvio Palmitano
el 17/11/16Recuerda que llamamos radio (R) a la distancia entre un vértice y el centro, y que llamamos lado (L), a la distancia entre dos vértices del triángulo.
Recuerda que en un triángulo equilátero tienes tres radios iguales, y tres lados iguales.
Luego, tenemos los datos del enunciado:
Centro: z = -2 + 3i.
Vértices: z1 = - 1 + i, z2 = a + bi, z3 = c + di, con a, b, c, d números reales a determinar.
Luego planteamos:
a) Para los radios: |z1 - z| = z2 - z|| = |z3 - z|, reemplazamos, operamos y queda la doble igualdad:
|1 - 2i| = |(a + 2) + (b - 3)i| = |(c +2) * (d - 3)i|, elevamos al cuadrado en los tres miembros de la doble igualdad:
|1 - 2i|2 = |(a + 2) + (b - 3)i|2 = |(c +2) + (d - 3)i|2, expresamos los módulos en función de las partes reales e imaginarias:
(1 + 4) = (a + 2)2 + (b - 3)2 = (c + 2)2 + (d - 3)2,
luego, tenemos dos ecuaciones, ambas con el primer miembro de la doble desigualdad:
(a + 2)2 + (b - 3)2 = 5 (*)
(c + 2)2 + (d - 3)2 = 5 (*)
b) Para los lados: |z2 - z1| = |z3 - z1| = |z3 - z2|,
reemplazamos, elevamos al cuadrado en todos los miembros y queda:
|(a + 1) + (b - 1)i|2 = |(c + 1) + (d - 1)|2 = |( c - a) + (d - b)|2, expresamos en función de las partes, y queda:
(a + 1)2 + (b - 1)2 = (c + 1)2 + (d - 1)2 = (c - a)2 + (d - b)2,
luego, tenemos otras dos ecuaciones, ambas con el primer miembro de la doble desigualdad:
(a + 1)2 + (b - 1)2 = (c + 1)2 + (d - 1)2 (**)
(a + 1)2 + (b - 1)2 = (c - a)2 + (d - b)2 (**)
Luego, con las ecuaciones señaladas y remarcadas (*) (**), tenemos el sistema de cuatro ecuaciones con cuatro incógnitas:
(a + 2)2 + (b - 3)2 = 5
(c + 2)2 + (d - 3)2 = 5
(a + 1)2 + (b - 1)2 = (c + 1)2 + (d - 1)2
(a + 1)2 + (b - 1)2 = (c - a)2 + (d - b)2
Luego, te queda la tarea de resolver este sistema de ecuaciones. Haz el intento y, si te es necesario, puedes volver a consultar.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/11/16Planteamos la ecuación característica:
r2 = (5/3)r - 2/3, multiplicamos por 3 en todos los términos y queda:
3r2 = 5r - 2, hacemos pasajes de términos y queda:
3r2 - 5r + 2 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son: r1 = 1, r2 = 2/3.
Luego, planteamos la expresión del elemento general de la sucesión:
Bt = c1*r1t + c2*r2t, con c1, c2 constantes reales que debemos determinar, t ∈ N, reemplazamos valores y queda:
Bt = c1*1t + c2*(2/3)t, resolvemos el primer término y queda:
Bt = c1 + c2*(2/3)t (*)
Luego, a partir del enunciado tenemos:
B0 = 300, reemplazamos y queda:
c1 + c2*(2/3)0 = 300, que al resolver el segundo término en el primer miembro queda (*):
c1 + c2 = 300 (**);
B1 = 200, reemplazamos y queda:
c1 + c2*(2/3)1 = 200, que al resolver el segundo término en el primer miebro queda (**):
c1 + (2/3)c2 = 200 (**)
Luego, con las ecuaciones remarcadas y señaladas (*) queda el sistema:
c1 + c2 = 300
c1 + (2/3)c2 = 200,
cuyas soluciones son: c1 = 0, c2 = 300.
Luego, reemplazamos en la expresión del elemento general de la sucesión, señalada (*) y queda:
Bt = 0 + 300*(2/3)t , cancelamos el término nulo y queda:
Bt = 300*(2/3)t , con t ∈ ℕ.
Observa que hemos respondido el inciso (b).
Observa que los incisos (a), (c) los puedes responder evaluando la expresión del elemento general.
Observa que en el inciso (d) debes plantear y resolver el límite del elemento general para t tendiendo a +infinito.
Observa que en el inciso (e) debemos calcular una suma de términos, que son elementos de la sucesión, a contar desde 0 hasta +infinito:
Σ(0 a +inf) Bt = Σ(0 a +inf) ( 300*(2/3)t ) = 300 Σ(0 a +inf) (2/3)t = observa que es una suma geométrica:
= 300 * 1/(1 - 2/3) = 300 * 1/(1/3) = 300*3 = 900.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/11/16Tienes planteada la ecuación de la recta r1: x + ay = b, y que el punto de coordenadas A(2,3) ∈ r1, por lo que reemplazamos sus coordenadas y queda la ecuación: 2 + 3a = b (*).
a) Tenemos la ecuación de la recta r2: x + 3y = 7, y tenemos que r1 // r2, por lo que planteamos la relación entre coeficientes:
1/1 = a/3, de donde despejamos y tenemos: a = 3, luego reemplazamos en la ecuación señalada (*) y tenemos: 11 = b.
Observa que la ecuación de la recta quedó: r1: x + 3y = 11.
b) Tenemos la ecuación de la recta r2 del inciso anterior, pero ahora piden que la recta r1 sea parpendicular a ella, por lo que planteamos la relación entre coeficientes.
1*1 = - a*3, de donde despejamos y tenemos: a = -1/3, luego reemplazamos en la ecuación señalada (*) y tenemos: 1 = b.
Observa que la ecuación de la recta quedó: r1: x - (1/3)y = 1.
Observa que hemos empleado la relación entre coeficientes de las ecuaciones cartesianas implícitas de dos rectas:
r1: a1x + b1y = c1, y r2: a2x + b2y = c2:
Condición de paralelismo: a1/a2 = b1/b2.
Condición de perpendicularidad: a1*a2 = - b1*b2.
Espero haberte ayudado.
-
Hola chicos:
Me podrías echar una mano, por favor, es que no entiendo las Permutaciones con repetición. No entiendo por qué es la fórmula así ni cuando se deben de realizar. Con un vídeo o con lo que sea si alguien me lo podría explicar estaría encantado.
Pn a, b, c = n!/ a! b! c!
Gracias de antemano por la ayuda.


Antonio Silvio Palmitano
el 17/11/16Tienes n elementos para ordenar, interesan todos, pero tienes grupos de elementos indistinguibles. Vamos con dos ejemplos, para que veas:
1) ¿En cuántas formas se pueden ordenar las letras de la palabra MURCIELAGO?
Tenemos: n = 10 (tenemos a disposición diez letras)
Tenemos: k = 10 (debemos ordenarlas a todas)
No hay repetición
Si interesa el orden
Estas son las cuatro condiciones para plantear una permutación de n elementos.
Luego, tenemos: N = P(10) = 10! = 3628800 formas de ordenar.
2) ¿En cuántas formas se pueden ordenar las letras de la palabra AMALGAMADA?
Tenemos: n = 10 (tenemos a disposición diez letras)
Tenemos: k = 10 (debemos ordenarlas a todas)
SI hay repetición: cinco letras A, dos letras M (las letras repetidas no se distinguen), por lo que tienes una clase con k1 = 3 elementos, y otra clase con k2 = 2 elementos, y quedan otras tres clases unitarias (una legra L, una letra G y una letra D), por lo que tenemos k3 = k4 = k5 = 1.
Si interesa el orden.
Luego tenemos: P(10)5,3,1,1,1= 10! / ( 5! 2! 1! 1! 1! ) = 3628800 / ( 120*2*1*1*1 ) = 3628800 / 240 = 15120 formas de ordenar.
Espero haberte ayudado.
-


David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)