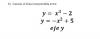-


Antonio Silvio Palmitano
el 10/11/16Para la continuidad, dices correctamente que la función es continua para todo número real, quedando para estudiar el punto de corte entre trozos: x = 0.
Para ello, planteamos la definición de continuidad en un punto:
a) f(0) = m*0 + n = n,
luego los límites laterales:
b) Lím(x-->0+) f(x) = Lím(x-->0+) (1-cosx)/x² = aplicamos la Regla de L'Hôpital:
= Lím(x-->0+) senx/2x = aplicamos la Regla de L'Hôpital:
= Lím(x-->0-+ cosx/2 = 1/2.
Lím(x-->0-) f(x) = Lím(x-->0-) (mx+n) = n.
c) Planteamos: n = 1/2.
Luego pasamos a la función derivada, que también tiene una expresión a trozos:
f ' (x) =
( -senx*x² - (cosx - 1)*2x )/x^4 = (-x*senx - 2cosx + 2)/x³ si x>0
m si x<0
Luego, tenemos que investigar si es posible la existencia de la función derivada en el punto de corte x=0, y para ello planteamos los límites laterales:
Lím(x-->0+) (-x*senx - 2cosx + 2)/x³ = aplicamos la Regla de L'Hôpital:
= Lím(x-->0+) (-senx - x*cosx + senx)/3x² = aplicamos la Regla de L'Hôpital:
= Lím(x-->0+) (-cosx - cosx + x*senx + cosx)/6x = Lím(x-->0+) ( - cosx + x*senx)/6x = aplicamos la Regla de L'Hôpital:
= Lím(x-->0+) (senx + senx + xcosx)/6 = 0.
Lím(x-->0-) (n) = n.
Luego planteamos: 0 = n.
Luego, la función derivada existe para x = 0, si y solo si: m = 1/2 y n = 0,
y para dichos valores, la función y su derivada son continuas en toda la recta real.
Espero haberte ayudado.
-
Hola unicoos, por favor espero me puedan ayudar con esto en algún video. Me piden Cómo se determinan y cuales son los límites trascendentes exponencial y logarítmico.
Espero su ayuda, muchas gracias.
-
una ayudita con esta ecuacion diferencial y'=2x-y+x2
determinar las regiones del plano en las cuales y'>0 y aquellas en las que y'<0


Antonio Silvio Palmitano
el 10/11/16Comencemos con el dominio de positividad de la función derivada:
y ' > 0, sustituimos y queda:
2x - y + x² > 0, hacemos pasajes de términos:
- y > - x² - 2x, multiplicamos por -1 en todos los términos de la inecuación (observa que cambia el sentido de la desigualdad):
y < x² + 2x, observa que es la región del plano xy que se encuentra estrictamente "por debajo" de la parábola de ecuación: y = x² + 2x.
Luego pasamos al dominio de negatividad, planteamos:
y ' < 0, sustituimos y queda:
2x - y + x² < 0, hacemos pasajes de términos:
- y < - x² - 2x, multiplicamos por -1 en todos los términos de la inecuación (observa que cambia el sentido de la desigualdad):
y>< x² + 2x, observa que es la región del plano xy que se encuentra estrictamente "por arriba" de la parábola de ecuación: y = x² + 2x.
Luego, pasamos a la ecuación diferencial, hacemos pasaje de términos y queda:
y ' + y = 2x + x², observa que es una ecuación lineal de primer grado y primer orden (te recomiendo mires los vídeos del tema),
luego, u solución general queda expresada:
y = e^(-x) * ( ∫ ( ( e^x * (2x + x²) )dx + C )
observa que queda para que resuelvas una integral por partes en dos pasos, como seguramente has visto en clase.
Espero haberte ayudado.
-


David
el 10/11/16Echale un vistazo... Distribución normal
A partir de ahí, sobre todo si tu duda es universitaria y debemos hacer una excepción... se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-) -
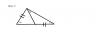
Lamento molestarlos y es que tengo problemas con el tema: congruencia de triángulos.....luego de intentarlo varias veces,quisiera que me guiaran con la resolución...

Ángel
el 10/11/16Parece un ejercicio típico con resolución a través del teorema del seno a/senA=b/senB=c/senC
¿Podrías revisar si el ángulo de 65º grados del triángulo de la derecha está copiado correctamente? ya que el ángulo x y el "otro" sólo sumarían 180-65=115º...el "otro" es claramente obtuso y sólo con él, ya tendríamos aproximadamente esos grados
De la forma que lo expusiste no sabría darte una solución (¿no te dan el valor de ningún lado?),
-
¿Cómo se resuelve la integral √x / x ?


Antonio Silvio Palmitano
el 10/11/16Observa que el numerador de la expresión de la función puede escribirse como potencia con exponente fraccionario:
√x / x = x^½ / x^1 = x^(½ - 1) = x^(-½), y luego integras como una potencia. Lo haces y queda:
∫ ( √x / x )dx = ∫ ( x^(-½) )dx = (2/3)x^(3/2) + C.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 10/11/16Observa que podemos escribir las ecuaciones paramétricas con los argumentos distribuidos:
x = 3t² - 2t³, de donde tienes: x ' = 6t - 6t²
y = 3t³ - 2t^4, de donde tienes: y ' = 9t² - 8t³.
a) Intersección con el eje OX: planteamos y = 0, sustituimos y queda:
3t³ - 2t^4 = 0, factorizamos y queda:
t³(3 - 2t) = 0, luego por anulación de un producto tenemos:
a1) t³ = 0, que nos conduce a t = 0, luego evaluamos:
x(0) = 0, y(0) = 0, y tenemos el punto: A(0,0).
a2) 3 - 2t = 0, que nos conduce a t = 3/2, luego evaluamos:
x(3/2) = 27/4 - 27/4 = 0, y(3/2) = 81/8 - 81/8 = 0, que nos conduce nuevamente al punto A(0,0).
Intersección con el eje y, planteamos x = 0, sustituimos y queda:
3t² - 2t³ = 0, factorizamos y queda:
t²(3 - 2t) = 0, luego por anulación de un producto tenemos dos opciones:
a3) t² = 0, que nos conduce a t = 0, luego evalúas y queda nuevamente el punto A(0,0).
a4) 3 - 2t = 0, que nos conduce a t = 3/2, luego evalúas y queda nuevamente el punto A(0,0).
b) Recta tangente horizontal: planteamos y '/x ' = 0, hacemos pasaje de divisor como factor, resolvemos y queda: y ' = 0, luego sustituimos y queda:
9t² - 8t³ = 0, factorizamos y queda:
t²(9 - 8t) = 0, que conduce a dos opciones:
b1) t² = 0, que conduce a t = 0, y al punto A(0,0).
b2) 9 - 8t = 0, y de aquí puedes despejar, luego evaluar las expresiones de x e y para determinar las coordenadas del punto (te dejo la tarea).
c) Recta tangente vertical: planteamos x '/y ' = 0, hacemos pasaje de divisor como factor, resolvemos y queda: x ' = 0, luego sustituimos y queda:
6t - 6t² = 0, factorizamos y queda:
6t(1 - t) =0, que conduce a dos opciones:
c1) 6t = 0, que conduce a t = 0, y al punto A(0,0).
c2) 1 - t = 0, y de aquí puedes despejar, luego evaluar las expresiones de x e y para determinar las coordenadas del punto (te dejo la tarea).
d) Evaluamos las expresiones de x e y para determinar el punto correspondiente a t = 1/2:
x(1/2) = 1/2, y(1/2) = 1/4, por lo que el punto correspondiente tiene coordenadas M(1/2,1/4).
Luego evaluamos las derivadas para encontrar el valor de la pendiente de la recta tangente:
x ' (1/2) = 3/2, y ' (1/2) = 5/4, luego planteamos para la pendiente de la recta tangente:
m = y ' (1/2) / x ' (1/2) = 5/4 / 3/2 = 5/6.
Luego, planteamos la ecuación cartesiana de la recta tangente.
y = (5/6)(x - 1/2) + 1/4.
Observa que para varias veces hemos llegado al punto de coordenadas A(0,0) con distintos valores del parámetro t, y eso significa que la curva se corta consigo misma en dicho punto.
Espero haberte ayudado.
-
Hola! he hecho este ejercicio para calcular el rango de una matriz.
Según la solución del libro debe dar rango=2, sin embargo creo que podría ser de rango 3...Ya que al calcular el determinante para rango 3 me da distinto de 0, me da 6 como se puede ver.
Que he hecho mal? agradezco una respuesta rápida ya que el examen es pronto.. gracias!!
PD: No he calculado el determinante por Sarrus si no por otro método que me enseñó mi profesor


Antonio Silvio Palmitano
el 10/11/16Observa que la fila 3 es la suma de la fila 1 con la fila 2. Luego, el rango no puede ser igual a 3, que es el mínimo entre el número de filas (3) y el número de columnas (4).
Luego, para investigar si el rango es igual a 2, puedes tomar, por ejemplo, los dos primeros elementos de las dos primeras filas, evalúas el subdeterminante formado con ellos, y verás que es distinto de cero, por lo que puedes concluir que el rango de la matriz es igual a 2.
Debes revisar tus cálculos al desarrollar los subdeterminantes de orden 3, porque si observas, en todos ellos la fila 3 es igual a la suma de las otras dos filas, por lo que todos los subdeterminantes de orden 3 son iguales a cero.
Espero haberte ayudado.