Asi Sergio  

Uno seria que los valores -2 y 0 no satisfacen la inecuacion adecuadamente por si te das cuenta reemplazando de quedara 3 < 3 o 1<1 lo cual no es correcto debido a que 3 no puede ser menor que 3  de esto que se concluye ...... aqui tu respuesta cuando se usa ''<'' y ''>'' quiere decir abierto  de modo que  en vez de usar corchetes simplemente usas ´´( ´´y ´´)´´ espero haberte ayudado 

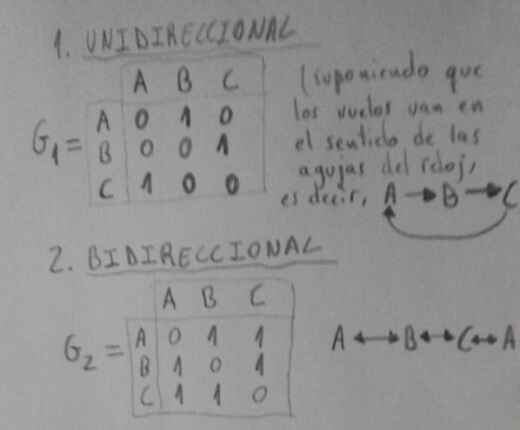
"al elevar al cuadrado G₁ invertimos el sentido de los vuelos)

(si a G₁ se le da el sentido unidireccional de las agujas del reloj, G₁² tendrá el sentido contrario a las agujas)

(si a G₁ se le da el sentido unidireccional contrario a las agujas del reloj, G₁² tendrá el sentido de las agujas del reloj)

*Recuerda que:

0+0=1+1=0  y  1+0=0+1=1

1*1=1  y  0*0=0*1=1*0=0

Al final del apartado 3 falta una flechita uniendo A--->C (para completar así el "ciclo del sentido" contrario a las agujas del reloj)

Echale un vistazo a los dos últimos apartados que quedan sin hacer y si sigues sin saber, te los paso en un momento 

Va una orientación. Observa que el cubo resultante tiene 3cm de arista, y está formado por tres "capas" de nueve cubos cada una.

Luego, observa que el cubo resultante tiene ocho vértices, y que los cubos correspondientes tienen tres caras pintadas (y por lo tanto otras tres sin pintar).

Luego, observa que en cada arista del cubo resultante hay un cubo intermedio, con dos caras pintadas (y por lo tanto otras cuatro sin pintar), y son doce cubos en total.

Luego, observa que en cada cara del cubo resultante hay un cubo central, con una cara pintada (y por lo tanto otras cinco sin pintar), y son seis cubos en total.

Luego, observa que en el centro del cubo resultante hay un cubo, que está rodado por otros cubos, y tiene todas sus caras sin pintar.

Queda para que hagas la tarea de verificar todo lo que hemos dicho, y sería muy conveniente que construyas, por ejemplo con dados o cubos de juego infantil, un modelo del cubo resultante.

Espero haberte ayudado.

Muchas gracias!!, practicaré lo que has dicho..

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

En tu caso te tocará aplicar CARDANO. 

Muchísimas gracias, me salvas la vida

Hagamos los cálculos término a término, si el cálculo a efectuar es el que indicas, tenemos:

5,22  + 0,33 = 27,04 + 0,027 = 27,067.

Luego, si los cálculos se realizan aproximando con la segunda cifra decimal (y le sumamos 1 si la tercera cifra decimal es 5 o más), tenemos:

5,22  + 0,33  ≅ 27,04 + 0,03 = 27,07.

Observa que en tu resultado no has colocado correctamente la coma decimal en el segundo término.

Observa que el cálculo que hicieron en clase corresponde al primer término solamente.

Espero haberte ayudado.

¿Entonces el resultado cuál es?

27,067 o 27,07, ya me lió más lo segundo de sumar uno porque tiene más de 5 cifras decimales... ¿o como?

PD: No funciona el botón de editar.

Lo volví a hacer y me sigue dando 2731, el dilema está también en donde tengo que colocar el decimal...

Yo hago lo siguiente: 5,2²+ 0,3³=       27,04 + 0,027 = 2731

Aaaaah, perdón... ya miré un vídeo en un programa de niños de como sumar con decimales jajaja, perdón perdón, me ha dado por fin un número más evidente, que es el siguiente: 27,067

¿Es entonces correcto?

¿Por qué la calculadora me da 0,027?

¿Qué quieres decir con esto?: Luego, si los cálculos se realizan aproximando con la segunda cifra decimal (y le sumamos 1 si la tercera cifra decimal es 5 o más), tenemos:

5,22  + 0,33  ≅ 27,04 + 0,03 = 27,07.

El resultado exacto es: 5,22  + 0,33 = 27,04 + 0,027 = 27,067.

Y el resultado aproximado con dos decimales; 5,22  + 0,33  ≅ 27,04 + 0,03 = 27,07.

Espero haber aclarado tu duda.

Tienes para la función:

g(x) = e^-2x, con g(0) = 1 = +2⁰

g⁽¹⁾(x) = -2e^-2x, con g⁽¹⁾(0) = -2 = -2¹

g⁽²⁾(x) = 4e^-2x, con g⁽²⁾(0) = +2²

g⁽³⁾(x) = -8e^-2x, con g⁽³⁾(0) = -8 = -2³

y en general:

g⁽ⁿ⁾(x) = (-1)ⁿ2ⁿe^-2x, con g⁽ⁿ⁾(0) = (-2)ⁿ

Luego, la expresión general de la Serie de McLaurin para esta función queda:

s(x) = ∑ ( (-1)ⁿ2ⁿ / n! )xⁿ, con n desde 0 a ∞.

Y la serie para la función del enunciado, observa que f(x) = xg(x), queda:

S(x) = ∑ ( (-1)ⁿ2ⁿ / n! )xⁿ⁺¹, con n desde 0 a ∞.

Luego, la derivada queda (observa que (xⁿ⁺¹)' = (n+1)xⁿ): 

S ' (x) = ∑ ( (-1)ⁿ2ⁿ (n+1)/ n! )xⁿ, que es la serie asociada a la función cuya expresión es: g ' (x) = (1-2x)e^-2x

Luego, pasamos al ejercicio:

a) Observa que la serie es S ' (1), que corresponde a: g ' (1) = - e^-2

b) Observa que 2²ⁿ⁺² = 2²ⁿ * 2² = 2ⁿ * 2ⁿ * 4 = 4*2ⁿ*2ⁿ, y que la serie es 4 * S ' (2), que corresponde a: 4 * g '(2) = 4(-3)e^-4 = -12e^-4

c) Observa que 2²ⁿ = 2ⁿ * 2ⁿ, y que la serie e S ' (2), que corresponde a: g '(2) = -3e^-4 = -3e^-4

Espero haberte ayudado.

a)

1) <0,0,0> ∈ V, porque para él: x + 2y - z = 0 +2*0 - 0 = 0.

2) Dados: u1 = <x1,y1,z1> ∈ V (observa que x1 + 2y1 - z1 = 0), u2 = <x2,y2,z2> ∈ V (observa que x2 + 2y2 - z2 = 0), planteamos:

u1 + u2 =<x1+x2,y1+y2,z1+z2> ∈ V porque par él:

x + 2y - z = x1 + x2 + 2(y1 + y2) - (z1 + z2) = distribuimos:

= x1 + x2 + 2y1 + 2y2 - z1 - z2 = ordenamos y agrupamos términos:

= (x1 + 2y1 - z1) + (x2 + 2y2 - z2) = reemplazamos según las igualdades remarcadas:

= 0 + 0 = 0.

3) Dado k ∈ R, planteamos:

k*u1 = k*<x1,y1,z1> = efectuamos el producto de escalar por vector = <kx1,kx2,kx3> ∈ V porque para él:

x + 2y - z = kx1 + 2ky1 - kz1 = extraemos factor común:

= k(x1 + 2y1 - z1) = reemplazamos según la primera igualdad remarcada:

= k*0 = 0.

Por todo lo que hemos desarrollado, tenemos que V es subespacio vectorial de R³.

b) Sea u = <x,y,z> ∈ (U ∩ V).

Luego, como u ∈ V, tenemos: x + 2y - z = 0.

Luego, como u ∈ U, tenemos: u = <x,y,z> = a<1,2,3> + b<2,-1,1> = < a+2b , 2a-b , 3a + b >, observa que x = a+2b, y = 2a-b, z = 3a+b, 

luego sustituimos en la ecuación anterior y queda:

a + 2b + 2(2a - b) - (3a + b) = 0, distribuimos y queda:

a + 2b + 4a - 2b - 3a - b = 0, reducimos términos semejantes y queda:

2a - b = 0, despejamos y queda:

2a = b, luego sustituimos en la igualdad remarcada y queda:

u = < a+2b , 2a-b , 3a + b > = 

= < a + 2*2a , 2a - 2a , 3a + 2a > = resolvemos componentes:

= < 5a , 0 , 5a > = extraemos factor escalar:

= 5a * < 1 , 0 , 1 >.

Por lo tanto, tenemos que los vectores u que son elementos del subespacio vectorial de R³: U ∩ V son múltiplos del vector < 1 , 0 , 1 >, por lo que una base de dicho subespacio es: B = { < 1 , 0 , 1 > }, y su dimensión es 1.

Espero haberte ayudado.