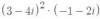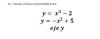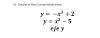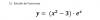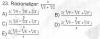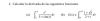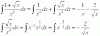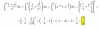-
Jeniffer
el 9/11/16Buenas tardes! en matemáticas empresariales estamos calculando curvas de nivel y no entiendo nada. Querría saber si hay por aquí algún curvas de nivel. Gracias!
-
Juan
el 9/11/16¿Quien me echa una mano con esta multiplicación den umero complejos?
Hugo
el 9/11/16
Antonio Silvio Palmitano
el 9/11/16Comencemos por el primer factor:
(3 - 4i)² = desarrollamos el binomio elevado al cuadrado:
= 3² + 2*3*(-4i) + (-4i)² = resolvemos potencias y productos:
= 9 - 24i + 16i² = resolvemos el cuadrado de la unidad imaginaria:
= 9 - 24i + 16(-1) = resolvemos el tercer término
= 9 - 24i - 16 = reducimos términos semejantes y queda:
= - 7 - 24i
Luego pasamos al producto del enunciado:
(3 - 4i)²(- 1 - 2i) = reemplazamos el primer factor:
= ( - 7 - 24i)(- 1 - 2i) = distribuimos:
= - 7(-1) - 7(-2i) - 24i(-1) - 24i(-2i) = resolvemos productos:
= 7 + 14i + 24i + 48i² = resolvemos el cuadrado de la unidad imaginaria:
= 7 + 14i + 24i + 48(-1) = resolvemos el último término:
= 7 + 14i + 24i - 48 = reducimos términos semejantes y queda
= - 41 + 38i.
Espero haberte ayudado.
-
Raisa
el 9/11/16Hola me podeis ayudar con estos ejercicios? Muchas gracias
4º Desde dos puntos A y B situados en la misma orilla de un río y distantes entre sí 80 m, se observa un punto C situado en la orilla opuesta, bajo ángulos de 60º y 45º, respectivamente. Calcula las distancias desde los puntos A y B al punto C.
(1,5 puntos)
5º Calcula los ángulos de un triángulo cuyos lados miden a=2cm; b=4cm; c=5cm
Antonio Silvio Palmitano
el 9/11/164°. Haz un dibujo, y verás que los tres puntos son los vértices de un triángulo, y las medidas de sus ángulos interiores son:
α = 60°, β = 45°, γ = 75°, para los ángulos con vértices A, B y C, respectivamente.
Luego, observa que el lado opuesto al vértice C, lo denominamos c, tiene 80m de longitud, y que nos preguntan las longitudes de los otros dos lados: b (opuesto al vértice B) y a (opuesto al vértice A).
Luego, a partir del Teorema del Seno podemos plantear dos ecuaciones
a) senα / a = senγ / c, de donde puedes despejar a = c*senα / senγ
b) senβ / b = senγ / c, de donde puedes despejar b = c*senβ / senγ
queda para que hagas los cálculos.
5°. Puedes aplicar el Teorema de las tangentes, y llamamos al semiperímetro del triángulo: p = (a+b+c)/2.
tan(α/2) = V( (p-b)(p-c) / p(p-a) )
tan(β/2) = V( (p-a)(p-c) / p(p-b) )
tan(γ/2) = V( (p-a)(p-b) / p(p-c) )
queda para que realices los cálculos.
Observa que este problema también puede ser resuelto si aplicamos el Teorema del Coseno.
Espero haberte ayudado.
-
Ángel
el 9/11/16Hola,
me ayudáis con este ejercicio?
f(x)= 5 + (x-1)4(x+2)3
Probar que:
a) f ´(x)=0 tiene al menos una solución en el intervalo (-2,1), sin calcular la expresión de f´.
b) f(x)=0 sólo tiene una solución menor que -2
c) f(x)=0 no tiene ninguna solución mayor que 1
Gracias
-
martin
el 9/11/16
Hola, en 2 días rindo un parcial de análisis matemático.. Tengo modelos de parcial que me dio el profesor, pero no se como resolver el calculo de áreas cuando una función es de grado 3, vimos un ejemplo en clase pero era mas simple que el del modelo del parcial.. Y tampoco se hacer el estudio completo de función de los ejercicios que están en el modelo de parcial también. Les paso los ejercicios y lo que pide el estudio de función, les agradecería si me puede ayudar.. :)
David
el 10/11/16Para el primero, echale un vistazo a todos los vídeos de esta leccion.. Area entre funciones 01
Para el segundo tienes decenas de vídeos. Desde los de ESTUDIO COMPLETO DE UNA FUNCION Estudio completo de una funcion racional
A los de DOMINIO, SIMETRIA, ASINTOTAS, CRECIMIENTO Y CURVATURA ....
Busca todos esos conceptos con el botón de busqueda...
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-) -
Daniel Macchiavello
el 9/11/16Comunidad buen dia me ayudan en este problema porfavor
Antonio Silvio Palmitano
el 9/11/16Llamemeos (indicamos raíz cúbica con (3V)): ² ³
a = (3V)(3), de donde tienes: a³ = 3 (*)
b = (3V)(2), de donde tienes: b³ = 2 (*)
Luego puedes apelar a la factorización de la suma de cubos que has visto en clase: (a + b)(a² - ab + b²) = a³ + b³.
Tienes la expresión: 2/(a + b) = 2/(a + b) * (a² - ab + b²) / (a² - ab + b²) = resolvemos el producto de expresiones fraccionarias:
= 2(a² - ab + b²) / (a + b)(a² - ab + b²) = aplicamos la factorización de la suma de cubos en el denominador:
= 2(a² - ab + b²) / (a³ + b³) = reemplazamos en el denominador a partir de las ecuaciones señaladas (*):
= 2(a² - ab + b²) / (3 + 2) = resolvemos en el denominador:
= 2(a² - ab + b²)/5, luego queda que sustituyas a y b, y verás que la respuesta correcta es la opción (A).
Espero haberte ayudado.
-
Albert einstein
el 9/11/16hola me podrian explicar como se resuelve el primer apartado, asi yo resuelvo el otro..
Antonio Silvio Palmitano
el 9/11/16Albert einstein
el 9/11/16
Antonio Silvio Palmitano
el 9/11/16Vamos con una idea acerca del Teorema Fundamental del Cálculo Integral (te recomiendo mires los vídeos sobre integracion).
Si tienes una función presentada como una integral, cuyos límites de integración son una constante y una función de x, tienes.
F(x) = Integral(entre a y u(x)) f(t)dt, entonces por el Teorema Fundamental del Cálculo Integral tienes que la derivada de la función queda:
F ' (x) = f( u(x) ) * u ' (x),
f(t) debe ser una función integrable entre los límites de integración planteados.
a) Tienes: f(t) = e^t / (3 + sent), y los límites de integración son: a = 1, u(x) = x, cuya derivada queda: u ' (x) = 1,
luego, por el Teorema Fundamental del Cálculo Integral, tenemos que la derivada de la función queda:
F ' (x) = e^x / (3 + senx) * 1 = e^x / (3 + senx).
b) Tienes f(t) = ( 1 + V(t) )/(2 + t), y los límites de integración son: a = 0, u(x) = x², cuya derivada queda: u ' (x) = 2x,
luego, por el Teorema Fundamental del Cálculo Integral, tenemos que la derivada de la función queda:
F ' (x) = ( 1 + V(x²) )/(2 + x²) * 2x = (1 + x)/(2 + x²) * 2x = resolvemos en el numerador = 2x(1 + x)/(2 + x²).
Espero haberte ayudado.
-
Esleyder
el 9/11/16Me pueden ayudar con este problema de circuitos lógicos? Se tiene una palabra de 5 bits, los últimos 4 bits representan un digito BCD, el primero es un bit de paridad impar (que significa esto, aclarenmelo porfa). Obtenga la tabla de la verdad y el pama de Karnaugh de las funciones siguientes: b).- F1 Se hará 1 para palabras con paridad incorrecta. Ok, mi duda no es que me resuelvan todo, lo que me pasa es que no entiendo a lo que el problema se refiere en lo que puse entre paréntesis. Y eso de palabras de paridad incorrecta, ni idea de que es. F2 supongo que se refiere a los valores de salida de la tabla de la verdad.
-
Albert einstein
el 9/11/16hola, alguien me podria explicar por que no se puede hacer esto en la siguiente integral? ∫(1/ 1+ x²) dx = ∫1+ x^-2 dx = ∫1 + ∫ x^-2 dx= x + x^- 1/-1= x -1/x , ya se que esa integral es del tipo arcotangente , pero porque esta mal esto? como distingo cuando se trata de un arcotangente? porque bien se puede elevar a la -1 y calcular la integral como polinomios? si me pudiera explicar lo agradeceria..
Antonio Silvio Palmitano
el 9/11/16Tienes que recordar que en una expresión fraccionaria se puede distribuir cuando el numerador es una suma, y el denominador está formado por un término único:
(a + b)/c = a/c + b/c.
Pero si el denominador está formado por dos o más términos, debe considerarse como un agrupamiento:
a/(b+c) no es distribuible.
El argumento de la integral es:
1/(1 + x²), y no es distribuible.
Sería muy conveniente que repases las propiedades con operaciones combinadas.
Espero haberte ayudado.
-
Fabricio
el 8/11/16Hola, genios de la vida. Me ayudan con ésta integral? he intentado resolverla por varios métodos, pero no me da igual al resultado que expresa el libro.
Muchas gracias.
