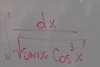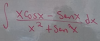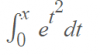-
Hola, buenas, tengo una duda.. es sobre una derivada que resolví y no estoy segura si está del todo bien, si me podéis ayudar corrigiendo y explicando en que fallé os lo agradecería! un saludo :)


Antonio Silvio Palmitano
el 6/11/16Debes repasar algunas reglas para simplificar (recuerda que en una expresión fraccionaria, no podemos simplificar un término del numerador con un término del denominador), pero si podemos simplificar factores:
(a + b)/(a + c) no es simplificable,
ab/ ac = b/c si es simplificable.
Luego, si la expresión de la función es:
y = ln( (x² - 1)/(x² + 1) ) = aplicamos la propiedad del logaritmo de una división y queda:
y = ln(x² - 1) - ln(x² + 1), luego derivamos término a término (observa que debemos aplicar la regla de la cadena:
y ' = ( 1/(x² - 1) )*2x - ( 1/(x² + 1) )*2x = 2x/(x² - 1) - 2x/(x² + 1) = extraemos factor común:
= 2x*( 1/(x² - 1) - 1/(x² + 1) ) = extraemos denominador común en el agrupamiento:
= 2x*( (x² + 1) - (x² - 1) ) / ( (x² - 1)(x² + 1) ) = resolvemos el segundo factor en el numerador:
= 2x * 2 / ( (x² - 1)(x² + 1) ) = resolvemos el numerador y llegamos a:
= 4x / ( (x² - 1)(x² + 1) ).
Espero haberte ayudado.
-
Que logaritmo da como resultado 1/2
Tengo que resolver la siguiente ecuación logarítmica y o se como igual logaritmos para poder quitarlos


Antonio Silvio Palmitano
el 6/11/16Recuerda la propiedad del logaritmo de una división: log(a) - log(b) = log(a/b) (indicamos logaritmo en base 4 como LOG):
LOG(x) - LOG(x-1) = 1/2, aplicamos la propiedad del logaritmo de una división):
LOG( x / (x-1) ) = 1/2, componemos con la función inversa del logaritmo en base cuatro (recuerda que es la función exponencial con base 4):
x/(x-1) = 4^(1/2), resolvemos a la derecha (observa que tenemos: 4^(1/2) = V(4) = 2):
x/(x-1) = 2, hacemos pasaje de divisor como factor:
x = 2(x-1), distribuimos a la derecha:
x = 2x - 2, hacemos pasaje de término y reducimos términos semejantes a la izquierda:
- x = - 2, multiplicamos en ambos miembros por -1 y llegamos a:
x = 2.
Espero haberte ayudado.
-

Tora Kevin Yack Quispe Tapia
el 6/11/16te recomiendo que estudies mas la parte de logica matematica
bueno al decir que si solo si entonces deben cumplir para ambos sentidos pero toma en cuenta que tienes un "o" que se traduce que si una parte de el segundo enunciado cumple no importa si el otro factor es falso tu afirmacion siempre sera verdadera

Antonio Silvio Palmitano
el 6/11/16Vamos con un esquema para la demostración:
1) (a+c)/(b+c) = a/b → a = b ∨ c = 0.
(a+c)/(b+c) = a/b → propiedad uniforme → b(a+c) = a(b+c) → propiedad distributiva → ba + bc = ab + ac → propiedad conmutativa → ab + bc = ab + ac → propiedad cancelativa →
→ bc = ac → luego tenemos dos opciones:
a) a = b, que nos conduce a: bc = bc,
∨
b) c = 0, que nos conduce a: 0 = 0.
2) a = b ∨ c = 0 → (a+c)/(b+c) = a/b
Tenemos dos opciones:
a) a = b → (a+c)/b+c) = sustituimos = (b+c)(b+c) = simplificamos = 1 = b/b = sustituimos = a/b;
∨
b) c = 0 → (a+c)/(b+c) = sustituimos = (a + 0)/(b + 0) = ley del elemento neutro de la suma = a/b.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 6/11/16Va una orientación.
Llamemos g(x) = 3mx² + (2m+4)x + (m-1), extraemos factor común en el término lineal y queda:
g(x) = 3mx² +2(m+2) + (m-1),
observa que se trata de una función polinómica cuadrática, y nos piden hallar m para que tome valores estrictamente positivos, por lo que necesitamos que la curva sea cóncava hacia arriba, y que su vértice se encuentre por encima del eje OX en un sistema de coordenadas cartesiano.
Luego, planteamos su derivada y su derivada segunda:
g ' (x) = 6mx + 2(m+2)
g ' ' (x) = 6m
Luego, como la gráfica debe ser cóncava hacia arriba, planteamos:
g ' ' (x) > 0, sustituimos y queda:
6m > 0, hacemos pasaje de factor como divisor, resolvemos y queda:
m > 0.
Luego, planteamos la condición de punto crítico (o singular):
g ' (x) = 0, sustituimos y queda:
6mx + 2(m+2) = 0, dividimos en todos los términos de la ecuación por 6m (recuerda que tenemos que m es estrictamente mayor que cero):
x + (m+2) / 3m = 0, hacemos pasaje de término, y llegamos a:
x1 = - (m+2)/3m.
Luego, planteamos que la ordenada del punto crítico (mínimo para nuestra gráfica) sea estrictamente positiva:
g(x1) > 0, sustituimos y queda:
3m( - (m+2)/3m )² + 2(m+2)( - (m+2)/3m ) + (m-1) > 0, luego operamos en los dos primeros términos y queda:
(m+2)² / 3m - 2(m+2)² / 3m + (m-1) > 0, luego multiplicamos por 3m en todos los términos de la inecuación (recuerda que 3m es estrictamente positivo) y queda:
(m+2)² - 2(m+2)² + 3m(m-1) > 0, reducimos términos semejantes y queda:
- (m+2)² + 3m(m-1) > 0, multiplicamos por -1 en todos los términos de la incecuación (observa que cambia el sentido de la desigualdad) y queda:
(m+2)² - 3m(m-1) < 0, luego desarrollas, reduces términos semejantes y queda:
- 2m² + 5m + 4 < 0, multiplicamos por -1 en todos los términos de la inecuación (observa que cambia el sentido de la desigualdad) y queda:
2m² - 5m - 4 > 0,
luego queda para que factorices y estudies los intervalos, como seguramente has hecho en clase.
Espero haberte ayudado.
-
Como puedo realizar él rango de esta matriz(31211) por gauss
11331
32112


David
el 7/11/16TRIANGULA LA MATRIZ COMO EN ESTE VÍDEO.. Sistema de ecuaciones con 4 incognitas Reduccion GAUSS
El rango será el numero de filas diferentes distintas de 0... -
Hola! Alguien me ayuda con la integral de e ^ ln x ? Muchas gracias, saludos.


Antonio Silvio Palmitano
el 6/11/16Debes tener en cuenta que las funciones: f(x) = e^x y g(x) = lnx son inversas entre si, por lo tanto: e^lnx = x, y también: ln(e^x) = x. Observa que el dominio en la función cuya expresión hemos escrito en negrita es el intervalo (0,+inf).
Luego, planteamos la integral:
∫ e^lnx dx = ∫ x dx = x² /2 + C.
Espero haberte ayudado.
-
Hola, necesito ayuda con esta integral, la intente por integracion por partes pero cada vez se hace mas grande. No se me ocurre otra manera


Antonio Silvio Palmitano
el 6/11/16Debes tener en cuenta que la función en el argumento de la integral no tiene primitiva elemental, y es por ese motivo que no podemos encontrarle una expresión a la integral.
Por favor, verifica en tus apuntes de clase, o en el enunciado del ejercicio, si te piden plantear la derivada de esta función, cuya expresión es la integral que figura en tu imagen.
Si este es el caso, estaríamos en condiciones de aplicar el Teorema Fundamental del Cálculo Integral, y queda:
F ' (x) = e^(x²).
Espero haberte ayudado.


Antonio Silvio Palmitano
el 6/11/16Si tienes a la integral en el numerador, y como denominador tienes a x, y el límite es para x tendiendo a cero, es tal como dices, aplicas la Regla de L'Hôpital, y para el numerador derivas por medio de la aplicación del Teorema Fundamental del Cálculo. Vienes muy bien encaminada (observa que si x tiende a cero, la integral en el numerador tiende a cero, porque tienden a igualarse los límites de integración):
la derivada del numerador queda: N ' = e^(x²), y la derivada del denominador queda: D ' = 1, por lo tanto, luego de aplicar la Regla de L'Hôpital, queda:
Lím(x→0) e^(x²) / 1 = e^0 = 1.
Espero haberte ayudado.