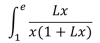-
Me ayudaís con este ejercicio que no sé ni como empezar por ser tres dados?
"Calcular la probabilidad de que la suma de puntos obtenidos en tres lanzamientos consecutivos de un dado sea cinco"
GRACIAS


Antonio Silvio Palmitano
el 7/11/16Observa que al lanzar el dado tienes 6 resultados posibles, y por cada uno de ellos tienes 6 resultados posibles al lanzar el dado por segunda vez, y por cada uno de los resultados obtenidos tienes 6 resultados posibles al lanzar el dado por tercera vez, por lo que tienes: N = 6*6*6 = 216 resultados posibles al lanzar un dado tres veces. Observa también que los lanzamientos son independientes (los resultados obtenidos en un lanzamiento no influyen en los demás).
Luego, los resultados favorables al evento "la suma de puntos en tres lanzamientos es cinco" son:
113 - 122 - 131 - 212 - 221 - 311, que son seis en total.
Luego, la probabilidad favorable al evento queda: p = 6/216 = 1/36.
Espero haberte ayudado.
-
Hola! Buenas noches.
Espero que me puedan ayudar con ejercicio que tomaron en un final de álgebra.
Hallas las raices cubicas del complejo z=(1) / (4 + 3i)
Desde ya muchas gracias.


Antonio Silvio Palmitano
el 7/11/16Primero, comencemos por expresar al número complejo en forma binómica, para ello multiplicamos al numerador y al denominador por el conjugado del denominador:
z = ( 1/(4+3i) )*( (4-3i)/(4-3i) ) = distribuimos y reslovemos = (4-3i)/25 = 4/25 - 3i/25.
Luego, observa que el número complejo está representado por un punto en el cuarto cuadrante, por lo que su argumento estará comprendido entre 270° y 360°, y su módulo es:
|z| = V( (4/25)² + (-3/25)² ) = V(25/625) = V(1/25) = 1/5.
Luego planteamos la tangente de su argumento:
tanα = (-3/25) / (4/25) = -3/4, luego componemos con la función inversa de la tangente y queda: α ≅ -36,87° + 360° = 323,13° = (≅ 0,90 radianes).
Luego, el complejo quede expresado en forma polar:
z = (1/5)(323,13°).
Luego, planteamos sus raíces cúbicas (las llamamos w):
w = (3V)(z) = (3V)( (1/5)(323,13°) ) = aplicamos la Fórmula de De Moivre:
= ( (3V)(1/5) )( (323,13° + 360°*k)/3 ), con k = 0,1,2 =
= ( 1 / (3V)(5) )(107,71° + 120°*k), con k = 0,1,2 = luego tenemos tres opciones:
a) w0 = ( 1 / (3V)(5) )(107,71°),
b) w1 = ( 1 / (3V)(5) )(227,71°),
c) w2 = ( 1 / (3V)(5) )(347,71°).
Espero haberte ayudado.
-
Hola, hace días me ayudaron a resolver un SEL con el método de Gauss Jordan, continué resolviendo los problemas pero también me aparece Gauss Seidel, para resolver este sistema:
debo hacer casi lo mismo que en el de Gauss Jordan?, sólo que en este me pide una tolerancia de 10-3
saludos !!


David
el 7/11/16Lo siento, no entiendo.. Debes aplicar lo mismo que yo en este video.. Sistema de ecuaciones con 4 incognitas Reduccion GAUSS
-
Hola, necesito ayuda con este ejercicio que no estoy tan seguro de que debo hacer:
-Demuestre que la recta normal a la grafica de x^3 + y^3 - 6xy = 0 en el punto (3; 3) pasa por el origen.
¿Debo derivar implicitamente o algo asi?
Gracias de antemano.


Antonio Silvio Palmitano
el 7/11/16Comienza por derivar implícitamente como afirmas y queda:
3x² + 3y² * y ' - 6y - 6xy ' = 0, luego evalúas para el punto de coordenadas (3,3) y queda:
27 + 27y ' - 18 - 18y ' = 0, luego reduces términos semejantes y queda:
9y ' + 9 = 0, luego despejas y llegas a:
y ' = -1, que es la pendiente de la recta tangente a la gráfica en el punto y, como la recta normal trazada en dicho punto es perpendicular, su pendiente queda:
M = -1/(-1) = 1, luego planteamos la ecuación cartesiana para la recta normal:
y - 3 = 1(x - 3), distribuyes a la derecha, cancelas términos y queda:
y = x, que es la ecuación cartesiana explícita de una recta que pasa por el origen de coordenadas.
Espero haberte ayudado.
-
Hola, necesito ayuda con el siguiente ejercicio:
Determine los intervalos de crecimiento de la funcion f(x) = x ln(x).
Gracias de antemano.


Antonio Silvio Palmitano
el 7/11/16Observa que el dominio de la función es D = (0,+inf), y que la función es continua y derivable en D.
Luego, planteamos la función derivada primera: f ' (x) = ln(x) + 1.
Luego planteamos la condición de punto crítico: f ' (x) = 0, que nos conduce a la ecuación:
ln(x) + 1 = 0, hacemos pasaje de término y queda:
ln(x) = -1, componemos en ambos miembros con la función inversa del logaritmo natural y queda:
x = e^(-1), que pertenece al dominio, y por lo tanto es un punto crítico (observa que e^(-1) ≅ 0,368).
Luego, subdividimos el dominio en intervalos, tomamos en cada uno de ellos un representante y evaluamos para él el signo de la derivada primera evaludada:
( 0 , e^(-1) ), representado por x = 0,1, y para él tenemos: f ' (0,1) = ln(0,1) + 1 ≅ - 1,303 < 0, por lo que la función es decreciente en este intervalo,
( e^(-1) , +inf ), representado por x = 1, y para él tenemos: f ' (1) = ln(1) + 1 = 0 + 1 = 1 > 0, por lo que la función es creciente en este intervalo,
y tenemos que la función presenta un mínimo en x = e^(-1), ya que en él pasa de decreciente a su izquierda a creciente a su derecha.
Espero haberte ayudado.
-
Una duda, si tengo una integral definida entre los respectivos extremos y realizo dos cambios de variable para resolverla, tengo que cambair dos veces dichos extremos de evaluacion. Gracia de antemano
-


Antonio Silvio Palmitano
el 7/11/16Puedes aplicar la sustitución (cambio de variable): w = 1 + L(x) (*), de donde tienes: dw = dx/x,
y también tienes: w - 1 = L(x), luego sustituyes y la integral queda (entendemos que L(x) indica logaritmo natural de x):
I = ∫ (w-1)/w * dw = distribuyes el denominador:
= ∫ (1 - 1/w)*dw = resuelves (observa que en los dos términos tienes integrales directas):
= w - L(w) + C = expresamos w en función de x a partir de la expresión señalada (*) y queda:
= 1 + L(x) - L( 1 + L(x) ) + C.
Espero haberte ayudado.
-
Hola buenas!! Me puede ayudar alguien con el siguiente problema:
Dos móviles salen del punto medio de la base de un triángulo equilátero con la misma velocidad constante.Uno recorre el perímetro y otro la altura (ida y vuelta) ¿Volverán a encontrarse?


Antonio Silvio Palmitano
el 7/11/16Llamemos v a la rapidez conque se desplazan ambos móviles, luego tenemos:
a) el móvil 1 recorre el perímetro completo (llamamos L a la longitud del lado del triángulo equilátero), por lo que su ecuación de movimiento queda:
vt = 3L, despejamos y queda: t = 3L/v, que es el tiempo que tarda en recorrer todo el perímetro,
y para calcular el tiempo que tarda en llegar al vértice opuesto a la base del triángulo (que es otro posible punto de encuentro) planteamos:
vt1 = 3L/2, despejamos y queda: t1 = 3L / 2v, que es el tiempo que tarda en recorrer todo el perímetro;
b) el móvil 2 recorre la altura (ida y vuelta), por lo que su ecuación de movimiento queda:
vT = V(3)L, despejamos y queda: T = V(3)L/v, que es el tiempo que tarda en recorrer la altura ida y vuelta,
y para calcular el tiempo que tarda en llegar al vértice opuesto a la base del triángulo (que es otro posible punto de encuentro) planteamos:
vT1 = V(3)L/2, despejamos y queda: T1 = V(3)L / 2v.
Luego compara, y verás que:
a) t ≠ T, por lo que no se encontrarán nuevamente en el punto de partida en la primera vuelta, y observa que t no es múltiplo entero de T, por lo que no se volverán a encontrar en dicho punto si continúan haciendo su recorrido indefinidamente.
b) t1 ≠ T1, por lo que no se encontrarán nuevamente en el vértice opuesto a la base del triángulo en la primera vuelta, y observa que t1 no es múltiplo entero de T1, por lo que no se volverán a encontrar en dicho punto si continúan haciendo sus recorridos indefinidamente.
Espero haberte ayudado.