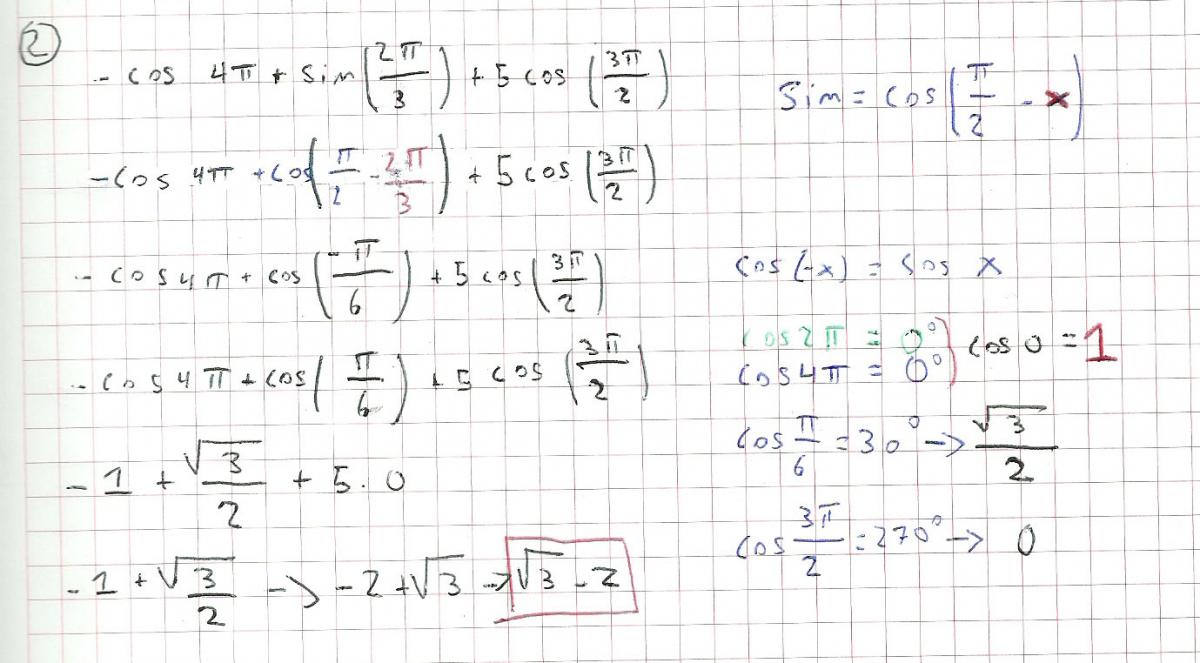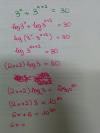-
-
Hola Unicoos, me he atascado, no sé como igualar las bases para poder resolver la x del exponente, como lo puedo hacer?
Me podrían echar una mano?

Ángel
el 26/10/16En la primera línea, si quisieras ponerlo en función de logaritmos tambien tendrias que aplicarlo al 30 del otro lado de la igualdad (cosa que no has hecho y por lo tanto es incorrecto)...entonces nos quedaria el log1030, que no nos conviene...ya que "un número que sea el exponente de 10 y nos dé como resultado 30" tiene decimales y nos lo complicaría más.
La manera de proceder sin complicaciones es sustituir 3x por una letra "a" y aplicar las propiedades de las potencia: EJEMPLO: 3x+2 = 3x * 32 = 3x * 9 = a * 9 = 9a
RESOLUCIÓN:
3x + 3x+2 = 30
a + 9a = 30
10a=30
a=3
a = 3x = 3 = 31 --------------> x=1
((puedes comprobar que el resultado es el correcto sustituyendo x=1 en la igualdad original: 31 + 31+2 = 30 ------> 31 + 33 = 30 --------> 3+27=30----> 30 =30))
-
Muy buenas Antonio, necesito tu ayuda ahí te va :
1- Resolver este sistema :
4x-y=2
raiz de x+1+ raíz de y-1=5
Ejercicio 3
Laura quiere hacer el marco de un cuadro con un listón de madera de 2 m sin que le sobre ni le falte nada. El cuadro tiene 24 dm2 de superficie. ¿Cuál es la longitud de los trozos que debe hacer?
Muchas gracias Antonio -
Hola Unicoos!!. Una consulta. Esta bien calculada la derivada de f(x)=1/(x^2+3) como f'(x)=(-1)/(x^2+3)^2 y la derivada segunda como f''(x)=(-4x)/(x^2+3)^4?.
Muchas gracias


Antonio Silvio Palmitano
el 26/10/16Observa que puedes escribir la expresión de la función como potencia con exponente negativo:
f(x) = (x^2 + 3)^(-1),
observa que tienes una composición de funciones (una potencia cuyo argumento es un binomio), por lo que debes derivar con regla de la cadena:
f ' (x) = - (x^2 + 3)^(-2) * 2x = ordenamos factores = -2x * (x^2 + 3)^(-2) (*);
luego, observa que tienes un producto, y en el segundo factor una composición de funciones, por lo que al volver a derivar queda.
f ' ' (x) = -2 * (x^2 + 3)^(-2) - 2x * (-2)*(x^2 + 3)^(-3) * 2x = operamos en el segundo término:
= -2 * (x^2 + 3)^(-2) + 8x^2 * (x^2 + 3)^(-3) = extraemos factor común:
= -2*(x^2 + 3)^(-3) * (x^2 + 3 + 8x^2) = -2*(x^2 + 3)^(-3) * (9x^2 + 3) = extraemos factor común numérico en el tercer factor y ordenamos factores:
= - 6*(3x^2 + 1)*(x^2 + 3)^(-3) (**).
Luego, si prefieres, puedes escribir las expresiones señaladas (*) (**) como expresiones fraccionarias, y quedan:
f ' (x) = -2x / (x^2 + 3)^2
f ' ' (x) = - 6(3x^2 + 1) / (x^2 + 3)^3.
Espero haberte ayudado.
-
Hola, pido ayuda a los profesor Antonio y César con este ejercicio de inducción, solo necesito saber cómo se opera la parte que está subrayada en rojo



Antonio Silvio Palmitano
el 26/10/16Observa bien en tu última línea, cuando aplicas la Hipótesis Inductiva, queda la expresión:
n*(n+1)! + ( (n+1)^2+ 1 )*(n+1)! = extraes factor común y queda:
= (n+1)! * ( n + (n+1)^2 + 1) = ordenamos y asociamos términos en el agrupamiento:
= (n+1)! * ( (n+1)^2 + (n+1) ) = extraemos factor común en el agrupamiento:
= (n+1)! * (n+1) * ( n + 1 + 1) = resolvemos el tercer agrupamiento y ordenamos factores:
= (n+2)*(n+1)! * (n+1) = multiplicamos los dos primeros factores, ordenamos factores y llegamos a:
= (n+1) * (n+2)!
Espero haberte ayudado.
-


David
el 26/10/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas
De ese tipo tienes varios vídeos que te vendrán genial... Los encontrarás en esta lección... ALGEBRA Matriz de Cambio de Base 01 -
Tengo: "raíz cuarta de 5625", y hay que sacar factores. Lo he hecho pero el resultado no coincide con el que dijo la profesora, alguien podria hacerlo? para asegurarme, gracias.
-
Hola, un ejercicio me pide calcular la derivada de Y cuando X es constante y viceversa:
1) F (X,Y) = 3X^2 + 5Y - 100
DERIVDA DE Y = 5
DERIVADA DE X = 6X
2) F(X,Y) = X^2/Y - /ln xy)^2
DERIVADA DE Y= -x^2/y - lnxy . 1/y
DERIVADA DE X= 2x/y - 2lnxy . 1/x
3) F (X,Y) = 10^3 (ln Y) + 5x^2 + 10Y
4) F (X,Y) = (In Y)^2/2 (ln x^3)/4
¿Cómo puedo hacer el apartado 3 y 4?
gracias

MDC
el 27/10/16El ejercicio fue dictado... pero lo que me pide es calcular en cada función la derivada de X suponiendo que Y es constante y al revés.
En el primer ejemplo al calcular la derivada de Y: Al ser X constante no tengo que derivarla y solo derivo "5y" que se quedaría en 5.
Pero no sé como hacer el apartado 3 y 4
-


Antonio Silvio Palmitano
el 26/10/16Debes expresar al vector genérico de R {3) como combinación lineal de los vectores <1,0,0>, <0,1,0> y <0,0,1> y luego transformar. Y como sabes que la transformación es lineal, recuerda que puedes transformar cada término por separado y,en cada término, puedes extraer el múltiplo escalar.
Tenemos:
<x,y,z> = <x,0,0> + <0,y,0> + <0,0,z> = x<1,0,0> + y<0,1,0> + z<0,0,1>.
Luego aplicamos la transformación, y sus propiedades:
f(x,y,z) = xf(1,0,0) + yf(0,1,0) + zf(0,0,1) = reemplazamos por los vectores transformados y queda:
= x<2,-1,1,1> + y<3,-1,1,0> + z<0,0,4,1> = resolvemos los productos entre escalar y vector en cada término:
= <2x,-x,x,x> + <3y,-y,y,0> + <0,04z,z> = resolvemos la suma entre vectores y llegamos a:
= <2x+3y,-x-y,x+y+4z,x+z>.
Por lo tanto, concluimos que la expresión para la transformación lineal es:
f(x,y,z) = <2x+3y,-x-y,x+y+4z,x+z>.
Espero haberte ayudado.