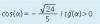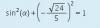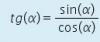-
En que cuadrante se encuentra?
Dada la ecuación sin2(x) + cos2(x) = 1
-Calcula el seno
Ahora calcula la tangente
-En principio el problema es fácil però por mucho que lo hago los resultados no me coinciden. Necesito ayuda, llevo horas atascado


Antonio Silvio Palmitano
el 26/10/16Observa que el coseno toma valores negativos en el 2° y en el tercer cuadrante, y la tangente toma valores positivos en el primer y en el tercer cuadrante, por lo tanto el ángulo A (alfa) pertenece al tercer cuadrante (observa que el seno toma valores negativos en este cuadrante).
Luego, a partir de la identidad pitagórica:
( cosA )^2 + ( senA )^2 = 1, reemplazamos y queda:
( -V(24)/5 )^2 + ( senA )^2 = 1, resolvemos el primer término y queda:
24/25 + ( senA )^2 = 1, hacemos pasaje de término:
( senA )^2 = 1 - 24/25, resolvemos a la derecha:
( senA )^2 = 1/25, hacemos pasaje de potencia como raíz (elegimos la solución negativa):
senA = - V(1/25), resolvemos y llegamos a:
senA = - 1/5.
Luego, planteamos la identidad trigonométrica para la tangente:
tanA = senA / cosA, reemplazamos y queda:
tanA = (- 1/5) / ( -V(24) / 5 ), resolvemos y queda:
tanA = + 1 / V(24), racionalizamos y llegamos a:
tanA = V(24) / 24.
Espero haberte ayudado.
-
Hola Unicoos. Me dan una mano con este ejercicio? No entiendo porque dice R2 y tiene 3 vectores, no necesito solo 2?? Porque lo que hice con los otros apartados del mismo ejercicio fue hallar la expresión de la transformación, haciendo por ej si era de R2 => (x,y) = x(u1) + y(u2). Pero aca tengo 3 vectores, no lo entiendo. Gracias!!


Antonio Silvio Palmitano
el 26/10/16Observa que el dominio de la transformación es R^2, que está formado por vectores de dos componentes reales, y que el codominio es R^3, que está formado por vectores de tres componentes reales.
Observa que podemos establecer la siguiente combinación lineal:
<5,2> = 2<1,1> + 3<1,0>
Luego, si suponemos que existe la transformación lineal planteamos:
f(5,2) = 2f(1,1) + 3f(1,0), luego reemplazamos a la derecha y queda:
f(5,2) = 2<2,1,1> + 3<0,2,0>, resolvemos los productos entre escalares y vectores y queda:
f(5,2) = <4,2,2> + <0,6,0>, resolvemos la suma entre vectores y llegamos a:
f(5,2) = <4,8,2>, que verifica la condición del enunciado, por lo que concluimos que si existe la transformación lineal.
Espero haberte ayudado.
-
-
inventa un polinomio de cuarto grado que tenga solo dos raíces : x=2 y x=-3


Antonio Silvio Palmitano
el 26/10/16Si el enunciado es que tenga solo esas dos raíces reales, entonces podría ser (observa que no está especificada la multiplicidad de las raíces):
P(x) = (x-2)(x+3)^3 (raíz simple: 2, y raíz triple: -3),
P(x) = (x-2)^2 * (x+3)^2 (raíz doble 2, y raíz doble: -3),
P(x) = (x-2)^3 * (x+3) (raíz triple: 2, y raíz simple: -3).
Espero haberte ayudado.
-
Muy buenas tardes unicoos. ¿Cómo podría saber el determinante de una matriz al cubo (det(A^3)), sabiendo que A es una matriz 3*3 cuyo determinante es 2 (det(A)=2)? Gracias de antemano.
-
1er ejercicio:
Inventa un polinomio de tercer grado cuyas raíces sean 3, -2 y -1
2do ejercicio:
inventa un polinomio de cuarto grado que no tenga raíces
¿Alguien que me sepa ayudar? Gracias de antemano
Ángel
el 26/10/16Para el primer ejercicio tienes que tener en cuenta que para obtener la raíz "3" tienes que poner el factor (x-3), para "-2" el (x+2) y para el "-1" (x+1)...entonces para obtener el polinomio de tercer grado que contenga esas tres raíces tienes que agrupar los 3 e igualar la ecuación resultante a 0, de manera que:
(x-3)(x+2)(x+1) = 0
multiplicamos 1er y 2º parentesis: (x2 + 2x -3x - 6) (x+1)
terminamos de quitar los paréntesis: x3 + x2 - x2 - x - 6x - 6 = 0
agrupamos para obtener el polinomio que nos pedían: x3 - 7x - 6 = 0