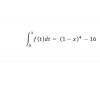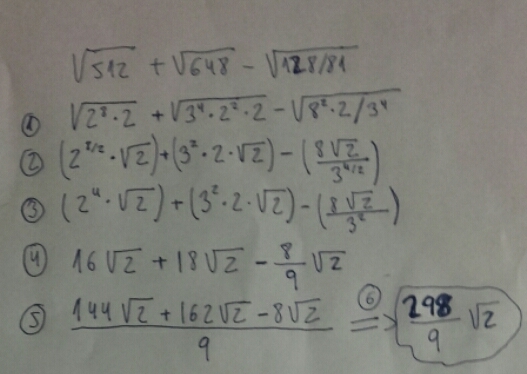-
Alguien me ayuda mas que nada con la parte de hallar el valor de a, no me sale. (el ejercicio tiene como letra (para poder enteneder un poco mas) Hallar f continua, el valro de a y el valor de la integral entre 0 y 1 de f.
-


David
el 24/10/16¿Has visto estos vídeos?... Combinatoria
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?


Antonio Silvio Palmitano
el 24/10/16Tal cuál sugiere David, te serán muy útiles los vídeos sobre el tema.
Vamos con algunas orientaciones:
1) Observa que el problema consiste en asignar (por ejemplo por sorteo) cuáles de los cuatro amigos tendrán su entrada, por lo tanto tienes:
n = 4 (tienes cuatro personas para elegir),
k = 2 (debes elegir dos de ellas para entregarles las entradas),
no interesa el orden en que designes a los amigos elegidos,
no hay repetición (cada amigo elegido tendrá una sola entrada para él),
por lo tanto, se cumplen las condiciones para plantear: C(4,2) = 4! / 2!2! = 6,
observa que si designamos A, B, C, D a los amigos, las opciones son: AB, AC, AD, BC, BD y CD, que son seis en total.
2) Observa que te quedan 20 preguntas para contestar, entre 30 preguntas que no son obligatorias, por lo tanto tienes:
n = 30 (tienes treinta preguntas no obligatorias a tu disposición),
k = 20 (debes elegir veinte de ellas para contestar),
no hay orden (puedes responder tus veinte preguntas en el orden que quieras),
no hay repetición (debes consignar una respuesta específica para cada pregunta),
por lo tanto, se cumplen las condiciones para plantear: C(30,20) = 30! / 20!10!,
observa que la cantidad de opciones es enorme, por lo que tendremos que confiar en nuestro planteo.
3) Para este problema, observa que la elección de discos no influye a la elección de libros que puedas hacer, observa que también se cumplen las condiciones para plantear combinaciones, tanto para la elección de discos como para la elección de libros, por lo tanto planteamos:
a) Elección de discos: n = 7, k = 3, sin orden, sin repetición, por lo tanto tenemos: N1 = C(7,3) = 7! / 3!4! = 35.
b) Elección de libros: n = 5, k = 2, sin orden, sin repetición, por lo tanto tenemos: N2 = C(5,2) = 10.
Luego, por el principio de multiplicación tenemos:
N = N1 * N2 = 35*10 = 350.
Observa que la cantidad de elecciones es grande, por lo que tendremos que confiar en nuestro planteo.
Espero haberte ayudado.
-


David
el 24/10/16Te sugiero TODOS LOS VÍDEOS de esta lección... ALGEBRA Matriz de Cambio de Base 01
A partir de ahí, me encantaría ayudarte, pero no podemos ayudaros en los foros con dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas
-


David
el 24/10/16Te sugiero los videos de funcion signo y de función parte entera... Despues, te tocará representar la función...
Función signo Función parte enteraSe trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?
-
bueno, ya no me rayo más. Tengo algún fallo en el ejercicios (o lo supongo) y no tengo ni idea de donde! Decirme donde fallo por favor! porque como tengo las dos ecuaciones primeras que son iguales menos el termino independiente sé que su rango no puede ser tres y me estoy haciendo un lío......

-
Buenas necesito ayuda con esta operación: √512+√648-√128/81 Es aplicando las potencias gracias!

sus
el 23/10/16descompón en factores primos y luego extrae siempre que sea posible.... el primer término de tu operación sería así: 512=29 Por lo que podrías extraer 24 de tu raíz cuadrada y dentro aún te quedaría otro 2. 24 √ 2
y así con los otros términos https://www.youtube.com/watch?v=n4LBiSxHv94
Espero haberte sido de ayuda. Ánimo
-
necesito ayuda con este problema de aplicación de derivadas dice así:
Un muro de 10 pies de altura está a 5 pies de un edificio, como se muestra en la figura. Encuentre la longitud L de la escalera más corta, apoyada en el muro, que llega desde el suelo hasta el edificio.
este es el link de la imagen
http://s1077.photobucket.com/user/Loperso/media/Escalera_zpsaiqso5pl.png.html

Antonio Silvio Palmitano
el 24/10/16Observa que, a partir de la imagen, puedes plantear dos triángulos rectángulos, con hipotenusas sobre la escalera, y con un mismo vértice en el punto de apoyo de la escalera en el suelo, tienes entonces (llamamos A al ángulo agudo que forma la escalera con el piso, expresamos las longitudes en pies):
Triángulo "pequeño" (base sobre el suelo, altura sobre el muro, hipotenusa sobre el tramo de escalera que va desde el punto de apoyo en el muro hasta el piso):
base = x,
altura = 10,
tanA = 10/x.
Triángulo "grande" (base sobre el suelo, desde la base del edificio hasta el punto de apoyo de la escalera en el piso, altura sobre la pared del edificio, desde su base hasta el punto de apoyo de la escalera sobre su pared):
base = x+5
altura = y
tanA = y/(x+5).
Luego, igualamos las expresiones para la tangente del ángulo A y queda:
y/(x+5) = 10/x, de donde despejamos:
y = 10(x+5)/x, distribuimos el factor y el denominador y queda:
y = 10 + 50/x (*).
Luego, planteamos para el cuadrado de la longitud de la escalera (f), a partir del triángulo "grande":
f = (x+5)^2 + y^2, luego sustituimos la expresión señalada (*) y nos queda:
f(x) = (x+5)^2 + ( 10 + 50/x )^2, desarrollamos los términos y queda:
f(x) = x^2 + 10x + 25 + 100 + 1000/x + 2500/x^2, reducimos términos semejantes y queda:
f(x) = x^2 + 10x + 125 + 1000/x + 2500/x^2 (**)
observa que tenemos el cuadrado de la longitud de la escalera en función de la distancia entre el pie del muro y el punto de apoyo de la escalera sobre el piso.
Luego derivamos:
f ' (x) = 2x + 10 - 1000/x^2 - 5000/x^3,
luego planteamos la condición de punto crítico (o singular), f ' (x) = 0 y queda la ecuación:
2x + 10 - 1000/x^2 - 5000/x^3 = 0, extraemos denominador común:
(2x^4 + 10x^3 - 1000x - 5000)/x^3 = 0, hacemos pasaje de divisor como factor (observa que nos queda cero a la derecha):
2x^4 + 10x^3 - 1000x - 5000) = 0, dividimos por dos en todos los términos de la ecuación:
x^4 + 5x^3 - 500x - 2500 = 0, extraemos factor común por grupos:
x^3 * (x + 5) - 500*(x + 5) = 0, extraemos al agrupamiento como factor común:
(x + 5)*(x^3 - 500) = 0, observa que por anulación de un producto tenemos dos opciones:
a) x + 5 = 0, de donde despejamos: x = - 5, que no es solución para nuestro problema, ya que x es una longitud y debe tomar valores positivos;
b) x^3 - 500 = 0, de donde despejamos: x = (3V)(500).
Luego, queda que reemplaces en la expresión señalada (**), recuerda que la función f expresa el cuadrado de la longitud de la escalera, extraes raíz cuadrada, y tienes la solución para este problema. Puedes verificar que la solución corresponde a un mínimo evaluando la expresión señalada (**) para un valor ligeramente menor que (3V)(500) y para otro valor ligeramente mayor que él.
Espero haberte ayudado.
-
Buenas, me podrian ayudar con el siguiente enunciado dado que estoy preparando un parcial, gracias. Dice asi:"Se ha observado que las cajas de cerveza se toman de los estantes de un supermercado a razon de 10 cajas por hora durante el periodo de mayor venta, siguiendo una distribucion de poisson, ¿cual es la probabilidad de que no se saquen cajas durante los primeros 7 minutos de un periodo de mayor venta?"