-
Fredy Morales
el 23/10/16Buen dia profe necesito su ayuda
Con esta simple ecuacion
8-5/x=2+3/x
mi procedimintosuponiendo que mi denominados queda x2
8x2-5x=2x2+3x
8x2-2x2-5x-3x6x2-8x
Luego no se que hacer!!
-
Beatriz Andrada
el 23/10/16Hola, profes! Necesito encontrar el valor de n. La fórmula es la siguiente: 3125= 50.000 * i (1+0.0196)n/(1+0.0196)n -1 Es urgente! Intenté resolverlo por logaritmos. Muchas gracias!
-
Gabriel
el 23/10/16Partiendo de la integral de x.arcsen(x)dx..haciendo los pasos para integracion por partes, llego a una integral de esta forma x^2 /raiz cuadrada de 1-x^2 dx (integral de equis al cuadrado sobre raiz de uno menos equis al cuadrado).Estoy trabado ahi mismo, nose como hacer para resolver esa integral.Por sustitucion no se puede, pasando el denominador arriba tampoco...hay otro mecanismo que estoy obviando?
-
Lorena Llanos
el 23/10/16 -
Carlos Ojeda
el 23/10/16
Hola, he intentado hacer este ejercicio de inducción, díganme dónde fallo por favor. Gracias
-
Antonio
el 22/10/16Alguien me ayuda con estos dos apartados?LLevo ya 2 horas y me estoy volviendo loco,gracias de antemano
-
Usuario eliminado
el 22/10/16 -
Carlos Ojeda
el 22/10/16Hola, tengo dos dudas con el álgebra de Boole: En la primera, no entiendo cuál es el paso que dan entre la primera y la segunda línea.
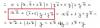
La segunda, es: si yo tengo y'.(x' + x ) + z ----- x' y x se anulan, pero no sé si y' (y negado) por 0 es y' o 0, ¿Es cierto y' . 0= 0?
Gracias
Antonius Benedictus
el 22/10/16Carlos Ojeda
el 23/10/16 -
Joship
el 22/10/16Hola Unicoos no me encuentro en esta probabilidad me podria ayuda por favor
Antonio Silvio Palmitano
el 23/10/16Primero observa que tienes dos experimentos independientes:
E1 : "se arrojan dos monedas", cuyo espacio muestral tiene cuatro elementos (indicamos los casos favorables en negrita):
CC, SS, CS, SC,
por lo que tenemos que la probabilidad de sacar dos caras o dos sellos es:
p1 = 2/4 = 1/2.
E2: "se arrojan dos dados", cuyo espacio muestral tiene treinta y seis elementos (indicamos los casos favorables en negrita):
11 12 13 14 15 16 - 21 22 23 24 25 26 - 31 32 33 34 35 36 - 41 42 43 44 45 46 - 51 52 53 54 55 56 - 61 62 63 64 65 66,
por lo que tenemos que la probabilidad de sacar un número en el primer dado que sea menor que el número del segundo en al menos en dos unidades es:
p2 = 10/36 = 5/18.
Luego, como los sucesos son independientes, tenemos:
p( S1 ∩ S2 ) = p1 * p2 = 1/2 * 5/18 = 5/36
Espero haberte ayudado..
-
aylen
el 22/10/16Hola únicos alguien me ayuda con esta derivada parcial? por favor
Antonio Silvio Palmitano
el 22/10/16Llamemos U = (p+q) / q^2 al argumento del logaritmo, luego sus derivadas parciales (observa que empleamos la regla del cociente) quedan:
Up = ( 1*q^2 - (p+q)*0 ) / q^4 = q^2 / q^4 = 1 / q^2.
Uq = ( 1*q^2 - (p+q)*2q ) / q^4 = ( q^2 - 2pq - 2q^2 ) / q^4 = ( - 2pq - q^2 ) / q^4 = q*( -2p - q ) / q^4 = ( -2p - q) / q^3).
También podemos escribir a la función como:
f(U) = lnU, cuya derivada queda: f ' (U) = 1/U.
Luego planteamos la derivada parcial primera de la función f con respecto a p (indicamos con (f)p):
(f)p = f ' (U) * Up = (1/U)*Up = ( q^2 / (p+q)) * ( 1 / q^2 ) = 1/(p+q).
Luego, volvemos a derivar con respecto a q (observa que empleamos la regla del cociente) para obtener la derivada segunda "cruzada":
(f)pq = ( 0*(p+q) - 1*1 ) / (p+q)^2 = -1 / (p+q)^2.
Puedes corroborar el resultado haciendo las derivaciones, primero con respecto a q y luego con respecto a p, y llegarás al mismo resultado, porque se cumple el Teorema de Claireaut.
Espero haberte ayudado.
