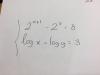-
Hola buenas Unicoos!
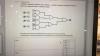
Agradeceria mucho una ayuda en este ejercicio de Algrebra de Boole, simplificación, tablas de verdad etc...
Un saludo y muchas gracias por adelantado!


David
el 25/10/16Me encantaría ayudarte, pero no respondo dudas universitarias o de asignaturas diferentes a matemáticas, FyQ que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas
Te sugiero, eso sí, todos estos vídeos... Puertas lógicas -
Hola Unicoos. Me dan una mano con este ejercicio?
" Encuentre la distancia mas cercana de v= (-1,-5,10) a W = gen {(5,-2,1), (1,2,-1)}"
La formula es ║v - proy(w)v ║
Pero como calculo la proyeccion de v sobre w??
-
Hola podrían ayudarme con este ejercicio tengo que hallar la ecuación paramétrica de la recta L que pasa por el punto Q(3,1,2) y es perpendicular a las rectas L1 = (1,0,2) + r(1,-2,2) y L2 = (2,6,-3) + t(3,0,-1) ya lo intente muchas veces y no me sale. gracias.


Antonio Silvio Palmitano
el 24/10/16Por favor, verifica que esté bien copiado el enunciado. Si es así, observa que el vector director de la recta L cuyas ecuaciones buscas debe ser perpendicular a los vectores directores de las rectas L1 y L2 (llamamos v1 y v2 a los respectivos vectores directores, luego tienes que el vector director de la recta queda:
v = v1 x v2 = < 2 , 7 , 6 >.
Luego, puedes plantear ecuaciones cartesianas paramétricas para la recta L:
x = 3 + 2w
y = 1 + 7w
z = 2 + 6w, con w perteneciente a R.
Puedes verificar que L no tiene intersección con la recta L1 y tampoco con la recta L2, por lo tanto resulta ser alabeada con ambas, no perpendicular a ellas.
Por lo tanto, no existe una recta perpendicular a L1 y L2 que pase por el punto Q, pero si existe un recta alabeada L cuyo vector director es perpendicular a los vectores directores de las rectas L1 y L2.
Recuerda que para que dos rectas sean perpendiculares, deben tener un punto en común y tener vectores directores perpendiculares. Y, para que una recta L sea perpendicular a otras dos rectas L1 y L2, debe cumplirse que las tres rectas tengan un mismo punto en común, y que el vector director de L sea perpendicular a los vectores directores de L1 y L2 al mismo tiempo.
Espero haberte ayudado.
-
hola unicoos, necesito ayuda con este ejercicio, se lo voy agradecer, muchas gracias. Desde Argentina


Alex Domínguez
el 24/10/16Mira en los vídeos de continuidad derivabilidad y teorema de Rolle en unicoos, te adelanto que no es dificil, simplemente en una hay que hacer los limites, en otra derivar y los limites y para el teorema de Rolle había un vídeo, simplemente eso, mirate los videos, espero ayudarte


Antonio Silvio Palmitano
el 24/10/16Observa que ambos trozos son continuos, y que debemos verificar la continuidad en el punto de corte a = 1:
a) f(1) = 1^2 = 1
b) Lím(x-->1-)f(x) = Lím(x-->1-)x^2 = 1,
Lím(x-->1+)f(x) = Lím(x-->1(2x - 1) = 2*1 - 1 = 1,
por lo que tenemos que Lím(x-->1)f(x) = 1
c) f es continua en a = 1;
por lo tanto concluimos que f es continua en [-3,5].
Planteamos la derivabilidad en (-3,5), observa que ambos trozos son derivables, por lo que tenemos:
f ' (x) =
2x si x < 1
2 si x > 1,
observa que los límites laterales de la función derivada para x tendiendo a 1 son ambos iguales a 2, por lo que podemos concluir:
f ' (x) =
2x si x < 1 (*)
2 si x = 1
2 si x > 1 (**),
por lo que f es derivable en el intervalo (-3,5).
Como tienes:
f es continua en [-3,5], f es derivable en (3,5), f(-3 = (-3)^2 = 9 y f(5) = 2*5 - 1 = 9,
se cumplen todas las hipótesis del Teorema de Rolle, entonces existe c perteneciente a (-3,5) tal que f ' (c) = 0.
Observa que c no puede ser igual a 1 porque ya vimos que f ' (1) = 2.
Observa que c no puede ser mayor que 1, porque para dicho puntos la función derivada toma el valor 2.
Luego, planteamos para el caso c < 1:
f ' (c) = 0, sustituimos a partir de la expresión señalada (*) y queda:
2c = 0, despejamos y llegamos a:
c = 0, que pertenece al intervalo (-3,5).
Espero haberte ayudado.
-


David
el 24/10/16¿has visto este video?... Sistema de ecuaciones logaritmicas
En tu caso, con la segunda log(x/y)=3... de donde 10³=x/y... 1000y=x....
Para la primera, no se me ocurre que hacer... ¿La has copiado bien? ¿no será una multiplicación en vez de una resta?.
Si fuera una multiplicación...2^(x+1+y)=8, que es 2³...
Y de ahí, obtendrías x+y+1=3... x+y=2... -
Hola, dejo aquí mi duda, aunque parezca de física solo quiero saber como resolver el sistema , lo he intentado y me da = 19'6 x (vo^2/a^2) pero me gustaria asegurarme, los sistemas son estos ;
0 = Ho – 4’9t2 y 0 = vot – 1/2at2
Gracias !!


Antonio Silvio Palmitano
el 24/10/16Si tus incógnitas son t y Ho, puedes comenzar por factorizar la segunda ecuación:
0 = t( Vo - (1/2)at ), de la que tienes dos opciones:
a) t = 0, luego reemplazas en la primera ecuación y tienes: 0 = Ho;
b) Vo - (1/2)at = 0, de la que haces pasaje de término y queda:
Vo = (1/2)at, luego haces pasajes de factores como divisores,, resuelves y queda:
t = 2Vo/a, luego sustituyes en la primer ecuación y queda:
0 = Ho - 4,9(2Vo/a)^2, resuelves el cuadrado y queda:
0 = Ho - 4,9*4Vo^2/a^2, luego resuelves factores numérico, hace pasaje de término y llegas a:
19,6Vo^2/a^2 = Ho.
Espero haberte ayudado.
-
Buenas tardes únicos tengo duda con estos dos ejercicios ,mi primo me los ha presentado al hacerlos ,el primer ejercicio lo he hecho,efectuando primero la operacion A*B y así he obtenido una matriz de orden 2*2,luego he hecho el determinanto obteniendo así los valores del parámetro M que son M=1 y M=-1,luego le he dicho que para estos valores no hay inversa,y que también el profesor suyo lo ha puesto mal,y dice que el lo ha puesto bien y así que no hay un error en la pregunta, y le he dicho que hay error en cuanto que dice que para que valores hay inversa.Por favor ayudarme tal vez yo estoy en el error.2 este ejercicio me dio parametros M=√7 y -√7 decirme si están bien estos ejercicios porfavor