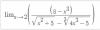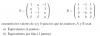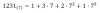-
hola que tal unicoos, podrían ayudarme con este ejercicio de combinaciones? lo he hecho de varias maneras pero no me da como debería dar en el libro, dice:¿cuantas manos diferentes de 8 cartas con 5 cartas rojas y 3 negras puede repetirse de una baraja de 52 cartas? la rta del libro es 171.028.000. gracias y saludos!!


Antonio Silvio Palmitano
el 24/10/16Observa que tenemos que, elegir sin orden 5 cartas rojas de un total de 26, y tres cartas negras de un total de 26, y observa que la elección de cartas de un color no influye en la elección de cartas del otro. Luego, vamos por pasos:
a) Elegimos las cartas rojas (diamantes o corazones): N1 = C(26,5) = 26! / 21!5!.
b) Elegimos las cartas negras (picas o tréboles): N2 = C (26,3) = 26! / 23!3!.
Luego, por el principio de multiplicación tenmos:
N = N1*N2 = C26,5)*C(26,3) = 171028000.
Espero haberte ayudado.
-
Que se puede hacer cuando se tiene este tipo de limites?
Nótese que las raices son distintas. Si intento la conjugada de la raiz cubica entonces la raiz cuadrada --> √(x2+5) queda asi (√(x2 +5))3 lo cual hace el ejercicio mas engorroso.
Gracias de antemano
-
Hola Unicoos:)
Os traigo una pregunta sobre espacios vectoriales.
Cuando me piden una base a partir de los vectores, no me queda claro cuando tengo que demostrar que es sistema generador y cuando no.
Se que para que sea base los vectores tienen que ser linealmente independientes y además sistema generador, pero tengo entendido (corregidme si me equivoco), que si el número de vectores que me dan coincide con la dimensión del espacio, no hace falta demostrar que es sistema de generadores y directamente se pasa a demostrar si son linealmente independientes, pero no entiendo porqué.
¿en qué casos tengo que demostrar entonces que es sistema generador y en cuales no?
Y ¿porqué cuando la dimensión del espacio coincide con el número de vectores, se sabe que es sistema generador directamente?
Gracias anticipadas:)


David
el 24/10/16Simplemente si la dimension de tu subespacio es 3 y tienes 3 vectores linealmente independientes, podrás generar cualquier vector en ese subespacio, pues puedes demostrar que cualquier vector es combinación lineal de los otros tres... Lo explico en este video un poco... No podría decirte más...
ALGEBRA - Base de un espacio vectorial -
Hola, primero comentarte , mi casó.
Tengo 35 años , me diras que mayor , pero, nunca tuve la oportunidad de estudiar . Y ahora estoy sacandome la eso , me han hecho un examen, y me an dicho que comenzaria a dar repasos de 1 de la eso .. y lo estoy haciaendo a distancia por trabajó ... Bueno... no entiendo las matematicas en problems cotidianos , me lio .pero si entiendo si me ponen un exame solo con numeros . Pero como me pongan, enunciados .. no entiendo nada . Soy muy torpe .Mil Gracias..


Nenúfar
el 23/10/16Hola Teresa:)
En primer lugar que sepas que no estás sola. Unicoos es una gran familia que te va a ayudar siempre que lo necesites.
Ante lo que dices de que te cuesta trabajo interpretar los problemas, te aconsejo que sigas los siguientes pasos:
1) Primero lee detenidamente el problema para ver de que va.
2.) Léelo por segunda vez y anota los datos que te dan y lo que te preguntan.
3.)Vuelve a leerlo comparando los datos que has apuntado con lo que hay en el enunciado para asegurarte de que pone lo mismo.
4. )Haz un dibujito si es necesario para que lo veas más claro
5.)Piensa en qué te piden y en los datos que tienes para llegar a ello. Y como puedes relacionar las dos cosas para tener la solución.
Cada problema es un mundo pero estos pasos te pueden ayudar a plantear todos los problemas.Luego simplemente mucha práctica. Al principio es normal que te lies, pero no te desesperes.No eres muy torpe, simplemente necesitas práctica. Roma no se construyó en un día. Con constancia y esfuerzo lo lograrás, no tengo la menor duda. Solo hay que ver como intentas superarte a tí misma para saber que esa es la actitud que hará que de aquí a unos meses nos estés contando tus logros.
Mucho ánimo Teresa, y para lo que necesites, ya sabes que aquí tienes una segunda familia para apoyarte y ayudarte en todo lo posible:)
-
Buenas tardes lluviosas! Podrian echarme una mano con este ejercicio? Se me complico al ser polinomios ;(



Antonio Silvio Palmitano
el 23/10/16Observa que puedes expresar a los polinomios (los ordenamos en forma decreciente) como vectores, en este ejercicio, de tres componentes:
v = <1,4,1>, p1 = <1,-2,5>, p2 = <2,-3,0>, p3 = <0,1,1>
Luego planteamos la combinación lineal particular para el vector v (a, b, c son números reales que debemos determinar):
ap1 + bp2 + cp3 = v, luego sustituyes, multiplicas número por vector en cada término y queda:
<a,-2a,5a> + <2b,-3b,0> + <0,c,c> = <1,4,1>,
luego planteamos un sistema de tres ecuaciones, componentes a componentes:
a + 2b = 1, de la que despejamos y queda: b = 1/2 - (1/2)a (*)
-2a - 3b + c = 4
5a + c = 1, de la que despejamos y queda: c = 1 -5a (**)
Luego sustituimos las expresiones despejadas en la segunda ecuación y queda:
- 2a - 3/2 + (3/2)a + 1 - 5a = 4, hacemos pasaje de término, reducimos términos semejantes y queda:
(-11/2)a = 9/2, hacemos pasaje de factor como divisor, resolvemos y tenemos: a = - 9/11 (***)
luego reemplazamos en las expresiones señaladas (*) (**) y tenemos: b = 1/2 + 9/22 = 10/11 (****), y también: c = 56/11 (*****).
Luego, reemplazamos los valores señalados (***) (****) (*****) en la combinación lineal que planteamos al comienzo y tenemos:
(-9/11)p1 + (10/11)p2 + (56/11)p3 = v.
Espero haberte ayudado.
-
alguien me podria ayudar con el siguiente ejercicio de matematicas? --- Demuestra que si A es una matriz cuadrada que cumple la relacion A^2 - A + I = 0 , sabiendo que A^-1 existe .Encuentra la expresion de la inversa de A .


Antonio Silvio Palmitano
el 23/10/16Observa que puedes hacer pasaje de términos y queda:
I = A - A^2, luego aplicamos propiedad de la matriz identidad que es neutro en el producto, y desarrollamos el cuadrado y queda:
I = A*I - A*A, luego extraemos factor común a izquierda en el segundo miembro y queda:
I = A*(I - A) (*)
Luego, a partir de la ecuación del enunciado, repetimos los pasos en forma similar (presta atención, porque trabajamos por el lado derecho en cada término):
I = I*A - A*A, luego extraemos factor común a derecha en el segundo miembro y queda:
I = (I - A)*A (**)
Luego, a partir de las expresiones señaladas (*) (**) tenemos que la matriz inversa queda:
A^(-1) = I - A.
Espero haberte ayudado.
-

Rafael Barbieru
el 23/10/1610011101 en base 2 (binario) sería el número 157. El proceso es bastante fácil, solamente te fijas en la cantidad de números que hay, en este caso son 8, y restas uno porque se empieza con 2^0. 8-1=7; elevas el 2 a 7 y te da 128. De allí colocas en órden todas las potencias menores: 128 64 32 16 8 4 2 1 y debajo de cada uno pones el número binario. Luego sumas los número decimales que tengan un uno del número decimal y eso te sale 157. También con la calculadora de windows si pones tu número decimal en la opción de programador y cambias a base 2 te lo da resuelto ya.
-


Antonio Silvio Palmitano
el 23/10/161) Observa que en el primer término puedes multiplicar y dividir por V(2) y queda:
(2*V(2))/(V(2)^2 = 2*V(2)/2 = simplificamos raíz y potencia en el denominador = 2*V(2)/2 = simplificamos = V(2).
Luego reemplazas, y la expresión del enunciado queda:
V(2) - V(2)/2 = extraes factor común = V(2)*(1 - 1/2) = resuelves el agrupamiento = V(2)*(1/2) = V(2)/2.
2) Observa que puedes multiplicar al numerador (N) y al denominador (D) por la expresión "conjugada" del denominador, y quedan:
N: 6*(V(7) - 2)
D: (V(7) + 2)*(V(7) - 2) = distribuimos = (V(7))^2 - 2*V(7) + 2*V(7) - 4 = cancelamos raíz y potencia en el primer término y cancelamos los términos centrales:
= 7 - 4 = 3.
Luego, escribimos la expresión:
N/D = 6*(V(7) - 2)/3 = simplificamos = 2*(V(7) - 2).
Espero haberte ayudado.