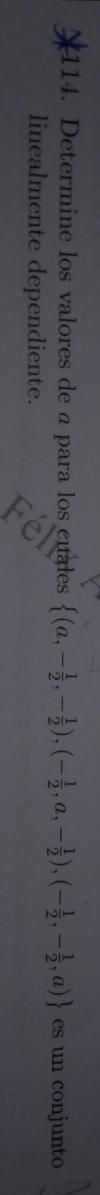Ya está disponible el nuevo portal donde podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios. Ir a beUnicoos

Ir a beUnicoos

Base de un espacio vectorial

Demostraremos si un conjunto de vectores forman una BASE de |R³ y las coordenadas de otro vector en dicha base. Para ello, hallaremos la dimension del espacio vectorial, que coincide con el numero de vectores linealmente independientes y el rango de la matriz que conforman los tres. Despues obtendremos las coordenadas de otro vector en esa base, desarrollando una combinacion lineal y resolviendo el sistema de ecuaciones resultante.

Agregar a mi mochila

0/ 773

* Para utilizar tu mochila o guardar tu progreso y acumular energy points debes ser usuario registrado. Regístrate o inicia sesión

Foro de preguntas y respuestas

Haz una nueva pregunta * Para dejar preguntas en el foro debes ser usuario registrado. Regístrate o inicia sesión

Marc Ramajo
el 29/11/19

Sería posible resolver el apartado "B" del ejercicio 18 ? me he es imposible resolverlo ...

••0 voto/s
•

Antonius Benedictus
el 29/11/19

•0 voto/s
•

Cancelar
KilledByLove
el 7/11/19

No entiendo el apartado b). Me explico, la resolución sí la entiendo ya que solo hay que sustituir. Lo que no entiendo es el enunciado; cuando dice "hallar las coordenadas de (2,4,6)", ¿a qué se refiere con ese (2,4,6)? ¿es un vector?
Cuando dice que hay que hallar unas coordenadas entiendo que se refiere a las coordenadas respecto a la base, pero yo tenía entendido que las coordenadas de un vector son las que vienen ya implícitas en este. ¿Quiere decir que las coordenadas del vector original que nos dan (2,4,6) son respecto al eje cartesiano o una base de vectores unitarios distinta a la base calculada en el ejercicio?
Espero que puedan entender mi duda, a veces a los alumnos nos cuesta explicar lo que no entendemos :/
Un saludo

••0 voto/s
•

Cancelar
luis Alberto Sanchez Ibarra
el 26/10/19

Buenas noches profesor queria saber si me podia explicar estos 2 ejercicios que no los termino de entender 😩😩

••0 voto/s
•

Breaking Vlad
el 28/10/19

se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)

•0 voto/s
•

Cancelar
KilledByLove
el 8/8/19

Buenas noches David, quisiera saber por qué le cambias el signo a la ecuación y=2α1-α2+α3 y la conviertes en y=2α1+α2+α3 No entiendo, eso fue muy gratuito, se supone que α2*(-1)=-α2 y de repente has borrado y le has cambiado el signo. Como diría Mourinho: ¿por qué? ¿por qué?

••0 voto/s
•

Breaking Vlad
el 16/8/19

Hola,
efectivamente se trata de una errata. Puedes comprobarlo en el apartado "errores en el vídeo"
Un saludo,
Vlad

•1 voto/s
•

Cancelar
Mony Guerreiro
el 5/8/19
Flag pendiente

Hola necesito ayuda con un ejercicio de transformacion lineal..

••0 voto/s
•

Breaking Vlad
el 16/8/19

Puedes preguntarnos cualquier duda que te haya surgido resolviendo problemas. Sólo ten en cuenta que nosotros NO resolvemos vuestros ejercicios, sino que os ayudamos a resolverlos por vuestra cuenta.

•0 voto/s
•

Cancelar
Maria Guadalupe Baltazar Castillo
el 15/6/19

••0 voto/s
•

Breaking Vlad
el 23/6/19

Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.

•0 voto/s
•

Cancelar
Ronald SucaTicona
el 7/6/19

••0 voto/s
•

David
el 26/6/19

Para dudas que no tienen que ver explicitamente con lo que hago en un vídeo, lo ideal es que uséis el FORO GENERAL de matemáticas, física o química

•0 voto/s
•

Cancelar
juan mendiondo
el 17/5/19

••0 voto/s
•

Antonius Benedictus
el 17/5/19

Lo antedicho sigue siendo válido.

•0 voto/s
•

Cancelar
juan mendiondo
el 17/5/19

••0 voto/s
•

Antonius Benedictus
el 17/5/19

Buenas tardes. Suba la duda al foro de Matemáticas, concretándola.

•0 voto/s
•

Cancelar
Yacer Franco Claros Choque
el 31/3/19

Hola espero que puedan ayudarme con este ejercicio

••0 voto/s
•

Antonius Benedictus
el 31/3/19

Súbelo al foro de Matemáticas, por favor.

•0 voto/s
•

Cancelar
Ana Laura
el 21/3/19

Hola tengo una duda me piden dado el conjunto de? 3 (-1, 0,2),(k-k,3)(0,-2,2),(2,0,-4) discutir para que valores de k es el conjunto de vectores un sistema de generadores de? 3.R3. Me podría ayudar o indicarme un video? He buscado pero la k me lía. Muchas gracias

••0 voto/s
•

Antonius Benedictus
el 21/3/19

Sube al foro de Matemáticas una foto del enunciado original, por favor.

•1 voto/s
•

Cancelar
Miguel
el 10/1/19

Hay un fallo que supongo que ya habrán comentado pero aviso por si acaso (no voy a leer todos los comentarios).
Al intentar saber si son un conjunto de generadores sin querer borra un menos (que estaba bien) en la segunda ecuación y pone un más que arrastra hasta el final del ejercicio sin darse cuenta modificando el resultado.
Espero que haya sido de ayuda.

••2 voto/s
•

Antonius Benedictus
el 10/1/19

OK

•2 voto/s
•

Cancelar
elizabeth mendoza de lavega
el 8/1/19

hola espero puedan ayudarme a resolver este ejercicio de estructura álgebraica

••0 voto/s
•

Antonius Benedictus
el 8/1/19

•1 voto/s
•

Cancelar
Sergio Arredondas
el 5/1/19

Hola buenas, podrían ayudarme con estos dos ejercicios?

••0 voto/s
•

Antonius Benedictus
el 5/1/19

•0 voto/s
•

Cancelar
Juan Pablo Garcia
el 29/10/18

hay un error aritmético en la y; debería ser y= 2a(1) -a(2)+a(3)

••1 voto/s
•

Antonius Benedictus
el 29/10/18

•0 voto/s
•

Cancelar
Natali Cardenas Almeida
el 24/10/18

Hola! Me podrías porfis explicar como se consigue un vector W3 de R3, para que los vectores W1=(2,-21,-3) y W2=(-4,16-3) formen base de R3 ? Y como se hace puede encontrar otro vector para q no sean base sin que sea el vector nulo?
Gracias!!!!

••2 voto/s
•

David
el 31/10/18

Para dudas que no tienen que ver explicitamente con lo que hago en un vídeo, lo ideal es que uséis el FORO GENERAL de matemáticas, física o química

•0 voto/s
•

Cancelar
William Núñez Noriega
el 17/10/18

Hola pueden resolver mi práctica porfabor

••0 voto/s
•

Antonius Benedictus
el 17/10/18

Sube tus dudas al foro de Mates, pero no os pidas que te hagamos el trabajo.

•1 voto/s
•

Cancelar
Isa
el 22/8/18

Tengo una duda, que no se si realmente puede ser contestada. A veces para entender las cosas necesito imaginarlas, así como se que una recta se forma con dos puntos, o un plano con dos rectas...
¿Qué es una base? "físicamente hablando" cómo se puede explicar, me ayudaría a entender que estoy haciendo realmente, pues en realidad lo hago de manera mecánica pero no se lo que es.
Muchas gracias

••3 voto/s
•

Antonius Benedictus
el 22/8/18

Una base es un conjunto de vectores (en número mínimo) que nos permiten obtener, combinándolos linealmente (mediante producto por escalares y sumas), cualquier vector. Esto es, cada vector de la base representa una dimensión (y un recta vectorial), por lo que en una base hay tantos vectores como dimensiones tiene el espacio vectorial correspondiente.

•4 voto/s
•

Cancelar
Lu Op
el 12/6/18

Me pueden ayudar con este ejercicio por favor¿? Me sale que no es diagonizable y no sé por qué. Gracias de antemano.

••0 voto/s
•

Guillem De La Calle Vicente
el 20/6/18

Si lo pones en el foro, te podremos ayudar. En los vídeos, tienes que poner dudas sobre los vídeos y no sobre ejercicios.
Saludos.

•1 voto/s
•

Cancelar
Javo
el 19/5/18

Buenas David, tengo una duda...
Alrededor del minuto 5:18 borras un signo negativo y lo pones en positivo, es una equivocación?
Porque a simple vista, si que deberia ser negativo, ya que multiplicas alfa2 por (-1), por tanto se queda negativo....
Gracias!

••0 voto/s
•

Antonius Benedictus
el 19/5/18

En fe de erratas (!) aparece esto:
Gracias por el aviso, Javo.

•0 voto/s
•

Cancelar
Clau Márquez
el 25/4/18

Así también se podría hacer el apartado b?

••2 voto/s
•

Antonius Benedictus
el 25/4/18

Sí, por supuesto.

•3 voto/s
•

Cancelar
pepi
el 24/4/18

Buenos días!

¿Cómo demostrar que se trata de subespacios vectoriales?
Gracias!

••0 voto/s
•

Antonius Benedictus
el 24/4/18

Sube al foro de Matemáticas la duda concreta.

•0 voto/s
•

Cancelar
Mark Anthony Ruiz Mendoza
el 8/4/18

En este ejercico no entiendo porque la respuesta correcta es la tercera, tenia entendido que la dimension de un polinomio era determinado por su grado mas uno, que en este caso seria 4, y por la tanto creia que era incorrecta. Se que la priemra opcion no es correcto porque la dimension de la matriz es 4, el segundo caso yo pensava que era el correcto y entiendo que el ultimo caso sea incorrecto porque hay vectores ld.

••0 voto/s
•

Antonius Benedictus
el 8/4/18

•0 voto/s
•

Cancelar
Leites Cruz Dámaris
el 8/3/18

Dibuja un sistema de referencia con dos ejes ( x,y ) ,que abarquen desde el _7 hasta el +7 en ambos ejes.

••0 voto/s
•

David
el 3/4/18

Lo siento pero no entiendo tu duda...

•2 voto/s
•

Cancelar
Jose
el 22/1/18

David, podrías hacer algún video más de espacios vectoriales??' De encontrar un vector...o de cualquier combinación..??
Gracias!!!

••0 voto/s
•

David
el 1/2/18

Si nos dejas algún ejemplo en el foro general de matematicas y aporta algo diferente a los que ya hay grabados, nos lo apuntamos. Abrazos!

•3 voto/s
•

Cancelar
Jaaziel Solano
el 20/1/18
- Si Hola a todos! Me pueden asesorar con este ejercicio? Se los agradecería mucho!
••0 voto/s
•

Antonius Benedictus
el 20/1/18

Súbelo al foro de Matemáticas. Es de números complejos.

•3 voto/s
•

Cancelar
Andrea Rubio
el 26/12/17

Hola, me podéis ayudar con este ejercicio?

••0 voto/s
•

Antonius Benedictus
el 26/12/17

•6 voto/s
•

Cancelar
aylen
el 12/12/17

Hola cómo se resuelve esto?

••0 voto/s
•

Antonius Benedictus
el 13/12/17

•0 voto/s
•

Cancelar
aylen
el 12/12/17

Buenas noches únicos!!! Me dieron este ejercicio para resolver...Ayuda por favor

•••0 voto/s
•

Antonius Benedictus
el 12/12/17

•0 voto/s
•

aylen
el 12/12/17

Muchísimas gracias!!!!

•0 voto/s
•

Cancelar
Irene
el 21/11/17

He intentado resolver este ejercicio pero la ecuación implícita por mucho que la hago no me sale igual y ya no se si me equivoco yo o el ejercicio esta mal.... me podrías evhar una mano resolviendolo por favor

••1 voto/s
•

Antonius Benedictus
el 21/11/17

Sube al foro de Mates una foto del enunciado original y lo miramos.

•1 voto/s
•

Cancelar
Carla
el 11/11/17

Hola, cómo puedo resolver el ejercicio para W3?

••0 voto/s
•

Antonius Benedictus
el 11/11/17

•1 voto/s
•

Cancelar
Carla
el 9/11/17

Hola, cómo puedo resolver estos ejercicios? especialmente el segundo, gacias.

••0 voto/s
•

Antonius Benedictus
el 9/11/17

•0 voto/s
•

Cancelar
Fabian
el 31/10/17

Por que cambias el signo de alfa2 en la y cuando despejas alfa3 en la Z?

••0 voto/s
•

Antonius Benedictus
el 31/10/17

Error contemplado en (!), debajo del vídeo.

•1 voto/s
•

Cancelar
Milena Canale
el 27/10/17

Si tengo una matriz 5x3 cual seria su rango si logro escalonarla sin ninguna fila de 0 ? puede ser L.I ?

••0 voto/s
•

David
el 29/10/17

Como mucho será 3..
Rango de una matriz por determinantes 01
•2 voto/s
•

Cancelar
Carlos
el 26/10/17

Perdona David,
Por lo que veo no se ha agregado mi pregunta. A ver ahora...
Saludos,
Carlos

••0 voto/s
•

David
el 29/10/17

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

P.D. En todo caso, para dudas que no tienen que ver explicitamente con lo que hago en un vídeo, lo ideal es que uséis el FORO GENERAL de matemáticas, física o química

•0 voto/s
•

Cancelar
Elena Peteiro
el 24/10/17

Dada la aplicación lineal que transforma él vector (0,2) en (0,3,0) y (0,4) en (4,0,0). Calcular núcleo e imagen (Sin matrices)

••0 voto/s
•

Antonius Benedictus
el 25/10/17

Pon foto del enunciado original en el foro. Esos datos no son correctos.

•2 voto/s
•

Cancelar
Carlos Fernandez
el 12/10/17

hola buenos días
¿podrias hacer un video de números imaginarios?
muchas gracias

•••3 voto/s
•

Nanilla Navarro
el 23/10/17

A mi tmbn me sería de mucha ayuda, gracias!

•0 voto/s
•

Antonius Benedictus
el 25/10/17

Numeros complejos 02 - Multiplicacion y division en forma binomica Numeros complejos 01 - Operaciones en forma polar

Numeros complejos 03 - De forma binomica a polar

Numeros complejos 04 - Raiz
•0 voto/s
•

Cancelar
Lautaro Aguirre
el 16/9/17

Chicos, podrian hacer un video de conicas, cilindros y superficies cuadraticas? Gracias por los videos me super ayudaron!

••0 voto/s
•

David
el 27/9/17

Ya tienes varios de conicas, pero no podemos ayudarte con dudas de nivel universitario, lo siento... espero lo entiendas.

•1 voto/s
•

Cancelar
Javier Guerra
el 31/5/17

No seria a2=-x/3+y/3-z/9??

••0 voto/s
•

Antonius Benedictus
el 31/5/17

El error está detectado. Haz click en el botón (!) debajo del vídeo.

•3 voto/s
•

Cancelar
Conchi De Francisco Simon
el 29/5/17

Los vectores da igual colocarlos en horizontal o vertical??

••1 voto/s
•

Antonius Benedictus
el 29/5/17

En principio, sí. Cuando se trabaja con la expresión matricial de una transformación lineal, se ponen como columnas.

•0 voto/s
•

Cancelar
Dana
el 18/5/17

no entiendo porque hay que comprobar que son un conjunto de generadores... no se supone que una vez hecho el determinante y comprobado que el rango es tres se acaba el ejercicio? Me refiero al primer apartado)

••0 voto/s
•

David
el 19/5/17

Si el rango es 3 son linealmente independientes, pero para que un conjunto de vectores sea una base también debe cumplirse que sean conjunto de generadores. Es posible que tu profe no lo considere imprescindible...

•4 voto/s
•

Cancelar
lourdes
el 10/5/17

y deberia ser: dos alfa 1 menos alfa 2 mas alfa 3, tienes un signo mal y todo mal no?

••0 voto/s
•

Antonius Benedictus
el 10/5/17

Mira la fe de erratas (botón ! debajo del video).

•0 voto/s
•

Cancelar
cyndi uribe
el 30/4/17

Hola David,
puedes hacer un video de aplicaciones lineales????

••5 voto/s
•

David Borrega Borrella
el 30/4/17

Lo apoyo!

•0 voto/s
•

Cancelar
Pablo Ramos Barahona
el 11/2/17

David, no deberia ser la tercera componente 8/3 ? no entiendo porque en los errores pones que da 0

••0 voto/s
•

Antonius Benedictus
el 11/2/17

Observación acertada,, Pablo. da mu=8/3

•1 voto/s
•

Cancelar
yassine
el 22/1/17

Eres el mejor señor David

••7 voto/s
•

David
el 24/1/17

:D Gracias!

•2 voto/s
•

Cancelar
sebastian mulato
el 30/11/16

hola queria hacer una pregunta en el minuto 5:17 , ¿por que cambia el signo menos por un mas o se equivoco ?

••0 voto/s
•

David
el 30/11/16

Revisa el apartado "errores en este vídeo", en la esquina inferior izquierda del reproductor
Un abrazo!

•1 voto/s
•

Cancelar
Lucas pajaro
el 25/11/16

Hola david buenos dias. Donde puedo encontrar el material adicional a este tema? Tengo un plan pro. Saludos.

••0 voto/s
•

David
el 29/11/16

No hay "material adicional" para contenidos universitarios, lo siento...

•0 voto/s
•

Cancelar
sabikara
el 5/11/16

perdona, y como harias para un caso en el que al menos uno de los vectores fuera linealmente dependiente y dos independientes?

••0 voto/s
•

David
el 7/11/16

En ese caso el rango sería dos. y la base estaría compuesta solo por los vectores linealmente independientes.. Pero sin ver el enuunciado literal no sabría que más decirte. Te sugiero lo dejes en el foro general de matemáticas.

•0 voto/s
•

Cancelar
maite271098@gmail.com
el 1/11/16

Buenas, podría explicar el método de Gram Schmidt por favor?

••0 voto/s
•

David
el 2/11/16

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Manuel Ortiz
el 22/10/16

Buenas tardes me podríantes dar algunas ideas para los siguientes problemas por favor
La primera es de determinar si el conjunto es espacio vectorial

De antemano gracias

•••0 voto/s
•

Nenúfar
el 22/10/16

Hola Manuel. Veo que eres nuevo en unicoos.En primer lugar, bienvenido :)
En segundo lugar, si quieres que te resuelvan dudas acerca de ejercicios, como es tu caso, tienes que dejarlo en el foro de la asignatura. Arriba en la pestaña foros, haz click en matemáticas y deja allí tu duda.
Estaremos encantados de poder ayudarte:)

•0 voto/s
•

David
el 24/10/16

Te ruego además que no dejes fotos dre 4 en 4, y que también al menos, las pongas en horizontal.
Tu duda se ha "apoderado" de todo el foro de este vídeo...

•0 voto/s
•

Cancelar
virginia
el 20/10/16

hola! donde se encuentra el material adicional?
gracias

••0 voto/s
•

David
el 24/10/16

En la esquina inferior izquierda del reproductor encontrarás "Preguntas", "Comentarios" y "Material adicional"... Solo puedes acceder a el si te apuntas a algunos de los planes PRO...

•0 voto/s
•

Cancelar
Carlos
el 17/3/16

David, en el minuto 5:18 borras el signo negativo de alfa 2 en "y" y por lo tanto cambia el resultado de todo el problema. Creo que lo cambias sin querer o no sé si lo cambias por algo. Un saludo.
•••2 voto/s
•

José Miguel
el 18/3/16

Hola Carlos, muy atento! Si miras los iconos en la esquina inferior izquierda del vídeo, el que tiene forma de X, pinchas y te especifica los errores que hay en el vídeo.
Saludos!
•2 voto/s
•

Loli
el 18/10/16

De todas formas al cambiar solo el signo de ese vector, es el mismo vector pero en el otro sentido. Con lo cual al resultado final no le afecta.

•0 voto/s
•

Cancelar
Catalina
el 5/3/16

No termino de entender porque haces el conjunto de generadores en el apartado a. Se que sirve para hacer el apartado b, pero ¿haciendo el conjunto de generadores se afirma que estos vectores constituyen una base de R³? ¿Por qué?

Gracias de antemano.
••0 voto/s
•

David
el 5/3/16

Son base si son linealmente independientes.... Lo explico en el video y en la descripcion. Te sugiero lo repases despacio..
•1 voto/s
•

Cancelar
Andrés Carreño
el 23/1/16

Muchas gracias por la clase. Tengo una duda, cuando pruebas si son conjunto de generadores (5:17), ¿dicho sistema de ecuaciones lo podría resolver por Gauss-Jordan, poniendo como matriz ampliada a soluciones X, Y , Z ?
••0 voto/s
•

José Miguel
el 24/1/16

Hola Andrés! Sí, se podría hacer perfectamente como dices. Pero lo más sencillo en este caso es como lo hace David ya que puedes despejar directamente el valor de un parámetro y sustituirlo en las otras dos ecuaciones.
Saludos!
•1 voto/s
•

Cancelar
juan
el 12/1/16

hola, tengo un problema con un ejercicio y es que ya vi todos los videos de álgebra (subespacio), también revise en el material adicional que por cierto esta muy bueno. pero aun no se como resolver este ejercicio; ¨encuentre la base de S={p ∈ P3 : p(0)=p(1)}¨
••0 voto/s
•

David
el 13/1/16

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

Por otro lado, para dudas que no tienen que ver explicitamente con lo que hago en el video, lo ideal es que useís el foro general de matematicas...
•0 voto/s
•

Cancelar
Alvaro Blazquez Marcos
el 25/12/15

Hola David estoy estudiando la carrera de Economia y en este tema de algebra estamos estudiando un apartado relacionado con el nucleo y la imagen y no tengo ni idea. Un ejercicio de ejemplo seria:
Calcular nucleo e imagen de f: R*4 ->R*3
(x,y,z,t) (2x+y+2z+t, 2x+3z+2t, -y+3t)

••0 voto/s
•

David
el 26/12/15

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas.

Por otro lado, para dudas que no tienen que ver explicitamente con el vídeo, lo ideal es que uséis los foros generales de matemáticas, física y química
•1 voto/s
•

Cancelar
Jack
el 15/12/15

Hola David, no tengo palabras para darte las muchas gracias por todo tu trabajo, me has ayudado muchísmo, fuí al bachillerato en mi país pero nunca estudiamos nada de los temas que tu tienes incluso en 4º de la eso, quiero preguntarte que es eso de "una base de R3"? que significa esa R? pero lo más importante, ¿qué tengo que estudiar para entender estos videos? he visto ya todos los videos de trigonometría, vectores, matrices, gaus, determinantes y sarrus, con tus videos he aprendido incluso a despejar y trabajar con fracciones, en mi época de estudiante tenía 10's en matemáticas, pero te prometo que nunca estudié el 90% de los temas que tratas en todos tus videos de mates.
••0 voto/s
•

David
el 16/12/15

R3 es el conjunto de todos los vectores en 3 dimensiones (x,y,z)
R2 es el conjunto de todos los vectores en 2 dimensiones (x,y)
¿mejor?
•2 voto/s
•

Cancelar
Amagel
el 29/11/15

NO ES UN ERROR !
En el min 2:00 al realizar el determinante, me han enseñado que es mejor realizar lo desarrollando por adjuntos cuando veo que una columna o fila esta llena de ceros, así ahorramos más tiempo en el examen.

det =3*(2+1)=3*3=9
••0 voto/s
•

David
el 30/11/15

OK!
•0 voto/s
•

Cancelar
alex
el 11/11/15

Sean U y V los subespacios de ¡3 generados por los vectores (1, 2, 1), (1,
3, 2) y (1, 1, 0), (3, 8, 5), respectivamente. Demostrar que U = V.
Podrias ayudarme

••0 voto/s
•

David
el 12/11/15

Para dudas que no tienen que ver explicitamente con el vídeo, lo ideal es que uséis los foros generales de matemáticas, física y química
Como pista, decirte que debes obtener las ecuaciones implicitas de cada espacio vectorial y comprobar que son linealmente dependientes... Dejanos, si quieres, todo lo que consigas (te sugiero el resto de videos de esta leccion) y te lo correjimos. Un abrazo!
•0 voto/s
•

Cancelar
Oscar
el 10/11/15

David te agradecería muchísimo que pudieras subir algún ejercicio de universidad de aplicaciones lineales. Ya se que no sueles subir mucho de universidad, yo te lo propongo por si más unicoos te lo han dicho ya y decides subirlo. De todas formas gracias por todo lo que haces por los estudiantes, nos has sacado de muchos lios jajaj
••4 voto/s
•

David
el 11/11/15

Tomo nota, te lo prometo. #nosvemosenclase
•6 voto/s
•

Cancelar
aftab
el 27/10/15

Hola soy un chico Pakistani casi llevo 4 años en españa y he aprobado el examen de selectividad con ayuda de tus videos gracias
Pero ahora en la Universidad es muy complicado Para mi estoy haciendo la ingenieria que hago to ports or dime

••0 voto/s
•

David
el 27/10/15

Hola!! Intentaremos siempre echarte un cable en los foros, pero unicoos por ahora se queda en bachiller, aunque haga excepciones de vez en cuando o muchos videos de bachiller puedan venirte muy bien... ANIMO!!!
•0 voto/s
•

Cancelar
Oscar
el 15/10/15

David, hoy mi profesor ha comentado que no va a hacer falta que sea un sistema generador para que sea una base. Que con que sea linealmente independiente y no se si algo más valía.... Conoces alguna otra opción para saber si varios vectores forman base?
un saludo y gracias por todo
•••0 voto/s
•

David
el 19/10/15

Lo unico que sé al respecto es lo que te he comentado. .. Y es la unica realidad...
•1 voto/s
•

Tiara Sánchez
el 3/12/15

En mi clase de álgebra lo que dicen es que serán base si los puedes expresar como conjunto de generadores, o sea como combinación lineal, (con alfa) mas o menos lo que has hecho tu, lo que pasa es que tal vez te confundas porque a veces no es necesario, o no te piden que compruebes todo el resto, pero si lo haces te servirá para los temas siguientes
•1 voto/s
•

Oscar
el 19/12/15

Maldita ingeniería xd
•0 voto/s
•

Cancelar
Leonardo Guerrero
el 6/10/15

Hola David buenos días, en estos tipos de ejercicios se puede sacar el mínimo común denominador?, veo que este ejercicio no haces eso.

saludos
•••0 voto/s
•

David
el 8/10/15

O minimo comun multiplo o comun denominador... Pero no mezcles conceptos ¿?ok?
•0 voto/s
•

Leonardo Guerrero
el 8/10/15

jeje Disculpame, pero en este tipo de ejercicio no se saca el minimo comun multiplo verdad?
•0 voto/s
•

Cancelar
octavio peña
el 27/9/15

Hola David
En el video en el minuto 5:18 borras el signo de alfa 2 y al volverlo escribir le cambias el signo
••2 voto/s
•

David
el 8/10/15

Sí... Lo siento... Dejé un monton de aclaraciones al respecto por culpa de ese fallo (puedes verlas en el icono de "errores" en la esquina inferior del reproductor
•2 voto/s
•

Cancelar
Kathia
el 4/9/15

Hola, tengo una duda, por ejemplo en R2 , yo tengo estos vectores (1,-3) (2,-5), yo saque la determinante y me salio a 1, eso es distinto a 0, pero ¿Significa que solo uno de esos dos vectores es Linealmente independiente? si es así ¿Significa que no es base?
••0 voto/s
•

David
el 8/9/15

Si el determinante es distinto de 0, los vectores serán LINEALMENTE INDEPENDIENTES ENTRE SÍ.... Y formarán una base en R²....
•1 voto/s
•

Cancelar
María José
el 30/6/15

Si me dan una W={landa, nu - delta, -nu, landa +delta} y me piden determinar si el vector (0,-2,1,1) pertenece a W y en caso afirmativo calcular las coordenadas del vector en la base obtenida en el apartado anterior. ¿Cómo lo hago? Gracias
••0 voto/s
•

David
el 30/6/15

Para dudas que no tienen que ver explicitamente con el vídeo, lo ideal es que uséis los foros generales de matemáticas, física y química
•0 voto/s
•

Cancelar
Carlos Garcia
el 27/5/15

David , ¿cómo se ponen los vectores al formar la matriz , veo que en el vídeo lo pones de manera horizontal , pero en algunos sitios he visto que lo ponen de manera vertical como adjunto en la imagen.
¿ Como se debe poner siempre , o daría igual ?
Gracias
••0 voto/s
•

David
el 28/5/15

Da igual que los pongas en vertical u horizontal. Lo importante es el rango de la matriz...
Y el rango no depende de ello (el rango de una matriz es igual al de su traspuesta).

•2 voto/s
•

Cancelar
Ezequiel Erick
el 9/5/15

Yo se que no tiene nada que ver pero necesito saber una resolucion como saber si son linealmente dependientes o independientes necesito saber eso.. por ejempo

x(2,2,3),y(6,7,8),z(5,6,6)
los pasos a seguir.. lei teoria pero no me queda claro

••0 voto/s
•

David
el 11/5/15

¿¿¿???? Lo explico en el vídeo...
Directamente, si su determinante es distinto de cero, el rango de la matriz que conforman será 3.. .Y los tres vectores serán linealmente independientes...

•0 voto/s
•

Cancelar
Natxo
el 27/4/15

¿La dimensión del espacio quiere decir R^3, o cuando se dice dimensión del espacio significa dimensión del subespacio?
Es que me lío con el espacio y subespacio y en determinados ejercicios he llegado a pensar que es lo mismo.
Gracias!
••0 voto/s
•

David
el 28/4/15

Un subespacio es un conjunto de vectores de R², R³, etc (ese sería el espacio vectorial de todos los vectores en dos o tres dimensiones) que cumplen una determina condicion... ¿mejor?
•2 voto/s
•

Cancelar
Yadara
el 24/4/15

Veo que estos ejercicios son todos de la UNIVERSIDAD, por tanto, no tengo que saber hacer esto para la selectividad ¿verdad?
Gracias
••0 voto/s
•

David
el 25/4/15

Tambien se da en bachiller, dependerá de la opción de matemáticas que estas estudiando...
Consulta tus libros, pero no suele caer en selectividad...
•1 voto/s
•

Cancelar
Amagel
el 8/4/15

Hola. EN EL MINUTO 5:15 HAS BORRADO LA ECUACIÓN DE Y (has puesto menos ALFA DOS). LA TENÍAS BIEN ANTES DE BORRAR.
Y=2ALFA UNO+ALFA DOS+ALFA TRES.
•••2 voto/s
•

David
el 8/4/15

Echale un vistazo al icono de "errores" (en la esquina inferior izquierda del reproductor)
BESOS!
•3 voto/s
•

Amagel
el 9/4/15

Ah vale Gracias. Todavía no me he acostumbrado a la página, acabo de enterarme de que hay un icono para ver los errores.QUE GRANDE!!!!
Gracias por avisarme. Un saludo.
•1 voto/s
•

Cancelar
AnthonellaPs
el 10/2/15

Tengo que hallar una base para el subespacio F= {(x,y,z,w)/x+y+z+w=0} en R4, ¿Cómo puedo demostrar que R4 esta contenido en F?
••0 voto/s
•

David
el 10/2/15

Para dudas que no tienen que ver explicitamente con el vídeo, lo ideal es que uséis los foros generales de matemáticas, física y química
Se trata, además de que enviéis dudas concretas, muy concretas (te sugiero veas antes el resto de vídeos de este tema). Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase

•0 voto/s
•

Cancelar
Giuliano
el 5/2/15

Transformaciones Lineales?
••0 voto/s
•

David
el 6/2/15

No, por ahora no... Lo siento...
•0 voto/s
•

Cancelar
Beatriz
el 16/1/15

¿Cómo se hace el cambio de base?
••0 voto/s
•

David
el 16/1/15

Echale un vistazo a los vídeos de matriz de cambio de base...
ALGEBRA Matriz de Cambio de Base 01
#nosvemosenclase
•0 voto/s
•

Cancelar
Raquel
el 9/12/14

Donde se pueden hacer los examenes. Es que soy nueva y no los encuentro

•••1 voto/s
•

Adrian Gamboa Cardenas
el 10/12/14

Examenes aqui, no hay; pero sería una buena idea para la web poder examinarse on line, en tiempo real, en una hora y fecha determinada, con toda la peña, tipo una maraton de "espacios vectoriales", acumulando de, no sé, puntos o estrellitas en el perfil... sería estimular a la practica grupal. Saludos
•8 voto/s
•

David
el 11/1/15

En teoría es una opción que está por incluir en un futuro, ya que te deberían dar 'medallas' por ello. A ver si lo hacen pronto! Saludos!
•0 voto/s
•

Iván Bielsa
el 28/5/15

Estaria bien

•0 voto/s
•

Cancelar
Micaela
el 9/12/14

Ahhh recién me doy cuenta de los otros errores. Voy a volver a hacer el ejercicio. En cuanto a la aclaración, significa eso que en R1 tendría un vector ya es base. En R2 dos vectores son base. Pero, no entendí por que 3 vectores no pueden ser base en R3. O sea, si dibujo tres vectores en una pizarra no son base en R2, pero ¿por qué no pueden serlo en R3?
Gracias por la ayuda:)
••0 voto/s
•

David
el 11/12/14

En R2 tendrás una base si tienes dos vectores LINEALMENTE INDEPENDIENTES ENTRE SÍ. Si tienes dos vectores, pero no son independientes entre sí, no tendrás base...
Del mismo modo, en R3 tendrás una base si tienes tres vectores LINEALMENTE INDEPENDIENTES ENTRE SÍ. Si tienes tres vectores, pero no son independientes entre sí, no tendrás base... Repasa el vídeo despacio, please
•1 voto/s
•

Cancelar
Micaela
el 9/12/14

¿Por qué cuando estaba resolviendo le cambio el signo a alfa 2(En el minuto 5:30 aprox.)?
¿Por qué tres vectores dibujados en la pizarra no constituyen base en dos dimensiones y por qué dichos vectores no constituyen base en 3 dimensiones?
••0 voto/s
•

David
el 9/12/14

En cuanto al error, échale un vistazo a los errores de este vídeo (en uno de los iconos de la esquina inferior izquierda del reproductor).
En cuanto a la condicion que deben cumplir determinado numero de vectores para constituir base es que sean linealmente independientes entre sí.
En |R2 (dos dimensiones) será imposible que encuentres 3 vectores linealmente independientes entre sí.
Del mismo modo, en |Rn (n dimensiones) será imposible que encuentres n+1 vectores linealmente independientes entre sí.
¿mejor?
•0 voto/s
•

Cancelar
Eliana Ventosinos
el 5/12/14

¡¡Hola!! ¿Qué tal? He encontrado un pequeño errorcito: y= 2alfa sub uno - alfa sub dos (es menos y no +) + alfa sub tres. =). ¡¡Está genial el nuevo sitio web!! ^_^.
•••8 voto/s
•

David
el 6/12/14

Ese día estaba "EMPANADO"! Muy muy atenta... Aunque ya sabía de mis errores y los había dejado explicados en youtube, aquí, en la nueva web, en este vídeo, no estaban apuntados. Así que, GRACIAS² !! Ahora, puedes verlos en uno de los iconos debajo del reproductor... Besos!
•4 voto/s
•

Eliana Ventosinos
el 6/12/14

=) De nada, es un gusto poder ayudar. ¡¡Genial!! Ya le he echado un vistazo =). ¡¡Saludos!!
•3 voto/s
•

Cancelar