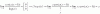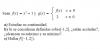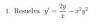-
aylen
el 24/10/16
-
Lau
el 24/10/16 -
Usuario eliminado
el 24/10/16Hola. El siguiente ejercicio me pide que estudie la derivabilidad de f(x). ¿Me lo podríais corregir?
-
Jefferson
el 24/10/16 -
Usuario eliminado
el 24/10/16Buenas, ¿podríais explicarme cómo se calculan los siguientes límites?
David
el 24/10/16Son limites exponenciales que se hacen aplicando el método logaritmico... Te sugiero... Limite Logaritmico
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok? -
Ángel
el 24/10/16Muchas gracias Antonio, como siempre :D
Tengo una última duda, que a lo mejor no tiene mucho sentido:
en el apartado B, por qué g(x) no tiene mínimo en f(0+) o f(0-) si es igual a 1+
o es porque tiene que llegar a un punto "único"? (como en el caso de f(x))
Espero haberme expresado bien
Un saludo
-
Ángel
el 24/10/16 -
José Manuel
el 24/10/16Necesito ayuda con esta ecuación de bernoulli
Antonio Silvio Palmitano
el 24/10/16Comienza con un pasaje de término y queda:
y ' - (2/x)y = - x^2 * y^2, luego multiplica en todos los términos por - y^(-2) y queda:
- y^(-2) * y ' + (2/x)*y^(-1) = x^2,
luego plantea la sustitución (cambio de variable): w = y^(-1), de donde tienes: w' = - y^(-2)*y ', sustituimos y queda:
w ' + (2/x)w = x^2.
Observa que tienes una ecuación diferencial lineal y de primer orden que puedes resolver, como seguramente has visto en clase.
Espero haberte ayudado.
-
Jessica Orjales Lázaro
el 24/10/16El ejercicio me dice que demuestre sin hallar el valor del determinante que los siguientes determinantes son multiplo de 5 y el determinante es:
1 15 6
5 -5 4
-2 20 7
He visto el video de youtube pero creo que no lo puedo aplicar a este determinante, graciasssss
-
Gustavo Fernández Jimenez
el 24/10/16Buenos días Benito:
Agradezco tu pronta respuesta a mi consulta del 17/10. He visto que al plantear la solución, el segundo término de la expresión que está dentro del paréntesis lo has tomado como si fuera x^2 y es 2^x. Esto cambia completamente el enfoque. Si no es molestia, te pido lo mires nuevamente y me orientes en la solución. Copio la pregunta que corresponde a un ejercicio para 1ro de Bachillerato:
Determina para qué valores de x es posible realizar la siguiente operación: log (x^2 - 2^x + 1).
Un saludo,
Gustavo
