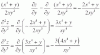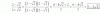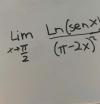-
-


Antonio Silvio Palmitano
el 22/10/16Observa que tienes a z como función de x e y, y que la expresión es:
f(x,y) = ( x^4 + y ) / (2xy^2) = distribuimos el denominador = x^4 / (2xy^2) + y / (2xy^2), simplificamos en cada término y queda:
f(x,y) = x^3 / (2y^2) + 1 / (2xy) = ordenamos factores en cada término, y escribimos potencias con exponente negativo en el numerador y queda:
f(x,y) = (1/2)x^3 * y^(-2) + (1/2) * x^(-1) * y^(-1).
Luego, observa que nos quedaron dos términos, y en cada uno factores constantes, factores con x y factores con y, por lo que se facilita la derivación.
Luego, si te piden la derivada tercera de z con respecto a y tres veces (observa que los factores que dependen de x son constantes), tenemos:
Derivada primera (la indicamos fy):
fy = - x^3 * y^(-3) - (1/2) * x^(-1) * y^(-2).
Derivada segunda (la indicamos fyy):
fyy = 3x^3 * y^(-4) + x^(-1) * y^(-3).
Derivada tercera (la indicamos fyyy):
fyyy = -12x^3 * y^(-5) - 3x^(-1) * y^(-4).
Espero haberte ayudado.
-
Buenas Unicoos tengo una duda que no consigo aclarar y es sobre radicales. la operación es 2-√2:2+√2. leído creo que queda dos menos raíz de dos dividido entre dos más raíz de dos. el resultado me da 3-2√2 y no consigo saber por qué gracias de antelación!!!
-
Buen día, por favor su ayuda con este caso de progresiones.
En un laboratorio, un científico después de aplicar un catalizador a una bacteria descubre que durante la primera hora obtuvo 3 bacterias y estas se reproducirán por tripartición cada hora, el científico requiere desarrollar en 8 horas un cultivo de bacterias superior a 50.000.
a) ¿Cuál es el tamaño del cultivo de bacterias obtenidas luego de las 4 horas?
b) ¿Logra el científico cultivar la cantidad de bacterias que requiere?
c) Independientemente de si lo logra o no lo logra ¿en cuánto tiempo lograría el científico tener el cultivo de bacterias requerido?
Gracias por su ayuda


jaime ignacio inostroza gonzalez
el 22/10/16mm si no me equivoco es una PA aplique la siguente formula an =a +( n-1)d en el cual reemplazaria y me quedaria asi 85 = 170+( n - 1) -2
lo cual me quedaria que n= 43 y la progresion es decreciente porque el peso lo quiere disminuir osea cada termino ira bajando saludos es la respuesta que creo yo si ahi algo malo corregirme ;)


Antonio Silvio Palmitano
el 22/10/16Llamemos f(t) a la cantidad de bacterias, transcurridas t horas desde el inicio del experimento. Observa que las bacterias se reproducen por tripartición, por lo que cada bacteria madre muere para dar nacimiento a tres bacterias hijas. Luego, tenemos:
f(0) = 1 (comenzó con una bacteria)
f(1) = 3 (transcurrió una hora desde el inicio, y ya tiene 3 bacterias)
f(2) = 9 = 3^2 (transcurrieron dos horas desde el inicio, y ya tiene 9 bacterias)
f(3) = 27 = 3^3 (transcurrieron tres horas desde el inicio, y ya tiene 27 bacterias)
observa que en general la expresión queda.
f(t) = 3^t, que es la cantidad de bacterias que tendrá cuando hayan transcurrido t horas desde el inicio del experimento.
a) f(4) = 3^4 = 81.
b) f(8) = 3^8 = 6561 < 50000, por lo que no se consigue el objetivo previsto por el científico a cargo del experimento.
c) Planteamos la ecuación:
3^t = 50000
tomamos logaritmos naturales en ambos miembros:
ln(3^t) = ln(50000)
aplicamos propiedad del logaritmo de una potencia:
t*ln(3) = ln(50000)
hacemos pasaje de factor como divisor y resolvemos:
t = ln(50000) / ln(3) = 9,85 (aproximadamente).
Por lo que concluimos que se alcanzará el objetivo cuando hayan transcurrido poco menos de 10 horas desde el inicio del experimento.
Espero haberte ayudado.
-
Hola Unicoos
¿Podrían decirme si lo que he realizado es correcto? En caso de que no lo fuese, ¿Podrían desarrollarme cómo se haría?


Antonio Silvio Palmitano
el 22/10/16Has operado correctamente en los incisos (b) y (c).
Observa que debes corregir en el inciso (a), y también completar:
a) 2V(2x-4) * 2V(2x-4) = ordenamos factores = 2*2 * V(2x-4) * V(2x-4) = expresamos como potencias = (2^2) * ( V(2x-4) )^2 =
resolvemos en el primer factor y cancelamos raíz y potencia en el segundo factor:
= 4*(2x-4) = 8x - 16 = extraemos factor común = 8(x - 2).
Espero haberte ayudado.
-
-


Antonio Silvio Palmitano
el 22/10/16Observa que tanto el numerador (N) como del denominador (D) tienden a 0 cuando x tiende a pi/2, por lo que el límite es indeterminado.
Una forma para resolverlo es aplicar la regla de L'Hôpital: Lím N/D = Líim N ' / D ' (*)
Derivamos:
N ' = cosx / senx
D '= 2(pi - 2x)(-2) = -4(pi - 2x).
Luego, planteamos el límite según la expresión señalada (*):
Lím(x-->pi/2) N ' / D ' = (-1/4) * Lím(x-->pi/2) cosx / (pi - 2x)senx = (**),
observa que el numerador y el denominador, ambos, tienden a 0, por lo que volvemos a plantear la regla de L'Hôpital:
N ' ' = - senx
D ' ' = -2senx + (pi - 2x)cosx.
Luego continuamos a partir de la expresión señalada (**):
= Lím(x-->pi/2) N ' ' / D ' ' = - 4 * Lím(x-->pi/2) ( - senx / ( -2senx + (pi - 2x)cosx ) = (-1/4)*( - 1/ (-2 + 0 ) = (- 1/4)*( -1 / -2) = ( -1/4)*(1/2) = -1/8.
Espero haberte ayudado.
-
Buenas alguien me podria decir si tengo bien este ejercicio o en que me he eauivocado y como corregirlo?
Tengo que discutir y resolver ese sistema
Gracias



Antonio Silvio Palmitano
el 22/10/16Observa que la compatibilidad determinada (única solución) del sistema de tres ecuaciones con tres incógnitas se decide, solamente, con verificar si el determinante de la matriz A es distinto de cero.
En este ejercicio, has calculado bien el determinante, te quedó que es igual a -4 que es distinto de 0, por lo que tenemos, sin más trámite, que el sistema es compatible determinado.
Luego, puedes escalonar y reducir la matriz ampliada A* que has planteado correctamente, con el método de las operaciones elementales por filas.
Haz el intento, y si es preciso, puedes volver a consultar.
Espero haberte ayudado.