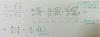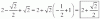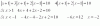-
lbp_14
el 22/10/16Hola Unicoos, esto lo han hecho antes más abajo por el foro y daba de resultado 3-√2 pero no entiendo ese método y yo lo he hecho a mi manera y no me da ese resultado . En qué he fallado?
Muchas gracias.
andres
el 22/10/16
lbp_14
el 22/10/16andres
el 22/10/16
Desencadenado
el 22/10/16 -
María Acosta
el 22/10/16 -
lbp_14
el 22/10/16Hola Unicoos ya sea en el numerador o denominador de una fracción, o en una simple ecuación normal, si me resulta más fácil cambiarles el signo como en este caso es incorrecto?
-
Jefferson
el 22/10/16Podrias ayudarme a resolver este ejercicio?
Sean la f (x) = e^2x y g (x) = -1/x^2 x2. Compruebe la regla de la cadena con las dos composiciones Posibles, es decir, demostrar que: - (f o g)'(x) = f'(g(x)) * g'(x) - (g o f)'(x) = g'(f(x)) * f'(x). Gracias!
Antonio Silvio Palmitano
el 22/10/16
Jefferson
el 23/10/16No me deja adjuntar la imagen, te dejo un enlace a la imagen con el enunciado.
https://www.dropbox.com/s/u0naakcdxkjq6sd/Captura.PNG?dl=0
Gracias!
-
Pablo Reyes
el 22/10/16Buenas noches, tengo todo el ejercicio resuelto. Si a = 3 dim V = 2 y su base (1,2,1,0) sin embargo me falta que si a ≠ 3 entonces dim v= 1 pero no sé sacar la base en función del parámetro 'a' ayuda por favor; sé que la duda corresponde a la universidad pero es que me urge.
-
Ana
el 22/10/16Hola, es un ejercicio de notación científica: Tengo que pasar el número 0.001 a algo similar a 10 elevado -algo. Mi profesor puso que sería 10 elevado a la menos tres pero no lo entiendo, no debería ser diez elevado a la menos cuatro?
Desencadenado
el 22/10/16
Antonio Silvio Palmitano
el 22/10/16Observa que tienes un número decimal finito, por lo que puedes escribirlo como una fracción decimal, en el que su denominador tiene como primera cifra a 1, seguido de una cantidad de ceros igual a la cantidades de cifras decimales que tienes a la derecha de la coma.
En tu caso tienes:
x = 0,001 = 1/1000 = escribimos al denominador como potencia de 10 = 1/10^3, expresamos como potencia con exponente negativo en el numerador y queda:
x = 1*10^(-3) = 10^(-3).
Si tuvieras:
y = 123,4 = 1,234*100 = 1,234*10^2.
z = 0,0678 = 6,78/100 = 6,78 / 10^2 = 6,78*10^(-2).
Siempre se busca expresar como el producto de un número con una cifra entera no nula, multiplicado por una potencia con base diez.
Otros ejemplos y explicaciones las puedes encontrar en los vídeos.
Espero haberte ayudado.
-
andres
el 22/10/16- Copiaste mal el ejercicio , siento muchísimo la molestia. escrito queda así mira 2-√2 ÷2+√2. Igual que como lo escribiste pero simplemente que el dos queda arriba con la raíz de dos al cuadrado. Si me puedes ayudar otra vez u otr@ unic@@ lo agradecería mucho.
lbp_14
el 22/10/16Hola Andrés, queda una fracción con raíz abajo, y para quitar esa raíz hay que racionalizar, para racionalizar se multiplica por el conjugado de la raíz que es el mismo sumando pero cambiado de signo arriba y abajo y quedaría así, espero que lo entiendas.
Creo que es así como se escribe según explicas.
-
Usuario eliminado
el 22/10/16Hola. Podríais corregirme el siguiente ejercicio?
6. Dado el número complejo z = 1 + i√3:
a) Calcule |z|, z, z2, arg z.
b) Obtenga un polinomio de grado 2 con todos sus coeficientes reales, tal que z sea raíz de ese polinomio. ¿Cuántas raíces tiene? ¿Cuáles son las otras?
Antonio Silvio Palmitano
el 22/10/16Tienes: z = -1 + iV(3), su parte real es x = -1, su parte imaginaria es: y = V(3), observa que está representado por un punto ubicado en el segundo cuadrante.
a) Módulo: |z| = V(x^2 + y^2) = V(1+3) = V(4) = 2.
Has planteado bien el conjugado: w = -1 - iV(3).
z^2 = ( -1 + iV(3) )^2 = (-1)^2 + 2*(-1)*iV(3) + i^2 * 3 = 1 - i2V(3) - 3 = -2 - 2V(3)i.
Tangente del argumento: tanA = y/x = V(3) / (-1) = -V(3), luego tenemos:
A = arctan(-V(3)) = 120° (= 2pi/3 radianes).
b) Recuerda que si un polinomio tiene todos sus coeficientes reales, puede tener todas sus raíces reales y, si tiene una raíz compleja, también tiene a su conjugada como raíz y con su misma multiplicidad.
Luego, como sabemos que z = -1 + iV(3) es raíz, por lo tanto tenemos que w = -1 - iV(3) también es raíz, por lo tanto planteamos la expresión general factorizada para un polinomio con dos raíces:
P(x) = (x - z)*(x - w) = distribuimos = x^2 - z*x - w*x + zw = x^2 - (z + w)*x + zw (*).
Luego calculamos los coeficientes:
-(z + w) = -(-1 + iV(3) - 1 - iV(3)) = cancelamos términos opuestos y reducimos términos semejantes = - (-2) = 2.
z*w = ( -1 + iV(3) ) * ( -1 - iV(3) ) = distribuimos y resolvemos = 1 - iV(3) + iV(3) + 3 = 4.
Luego, la expresión del polinomio, señalada (*) queda:
P(x) = x^2 + 2x + 4.
Espero haberte ayudado.
-
lbp_14
el 22/10/16Hola Unicoos, esto estaría correcto?
Muchas gracias
Antonio Silvio Palmitano
el 22/10/16Una recomendación.
Cuando llegas a la ecuación:
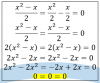
x^2 = x
observa que tienes dos términos, uno en cada miembro de la ecuación, por lo que no puedes despejar como hiciste, ya que te quedaron expresiones con incógnita en ambos miembros. Por lo tanto, haces pasaje de término y queda:
x^2 - x = 0
observa que puedes extraer factor común x en todos los términos del primer miembro de la ecuación, y que tienes a cero en el segundo miembro como único término:
x(x - 1) = 0
observa que nos quedó una ecuación con su primer miembro factorizado, e igualada a cero. Por lo tanto, por anulación de producto tenemos dos opciones, que son las que te indicó el colega César:
1) x = 0, que es una solución.
2) x - 1 = 0, de donde despejas y queda: x = 1, que también es una solución.
Por lo tanto, el conjunto solución queda: S = { 0 , 1 }.
Espero haberte ayudado.
-
jaime ignacio inostroza gonzalez
el 22/10/16hola amigos tengo la siguiente ecuación con valor absoluto |x+1|+3|x+1|+2|x-1|=10 quisiera saber si aplico los puntos criticos y tabla ?
Antonio Silvio Palmitano
el 22/10/16Observa que los dos primeros terminos son semejantes, por lo sumas y la ecuación queda:
4|x+1| + 2|x-1| = 10.
Luego, observa que en principio tenemos cuatro opciones, según la definición de valor absoluto:
1) x +1 >= 0 y x - 1 >= 0 y 4(x+1) + 2(x-1) = 10
2) x + 1 >= 0 y x - 1 < 0 y 4(x+1) + 2(x-1) = 10
3) x + 1 < 0 y x - 1 >= 0 y 4(x+1) + 2(x-1) = 10
4) x + 1 < 0 y x - 1 < 0 y 4(x+1) + 2(x-1) = 10
Cada una de las soluciones nos aportará parte de la solución, y las condiciones dentro de cada opción deben cumplirse simultáneamente. Luego despejamos en cada opción y tenemos:
1) x >= -1 y x >= 1, y la tercera: 4x + 4 + 2x - 2 = 10, de la que podemos despejar: x = 4/3, que cumple con las dos primeras condiciones, por lo que es parte de la solución.
2) x >= -1 y x < 1, y la tercera: 4x + 4 - 2x + 2 = 10, de la que podemos despejar: x = 2, que no cumple con la segunda condición, por lo que no es parte de la solución.
3) x < -1 y x >= 1, y la tercera: - 4x - 4 + 2x - 2 = 10, de la que podemos despejar: x= 8/3, que no cumple con la primera condición, por lo que no es parte de la solución.
4) x < -1 y x < 1, y la tercera: - 4x - 4 - 2x + 2 = 10, de la que podemos despejar: x = -2, que cumple con las dos primeras condiciones, por lo que es parte de la solución.
Por lo tanto, el conjunto solución queda: S = { -2 , 4/3 }.
Espero haberte ayudado.
