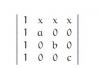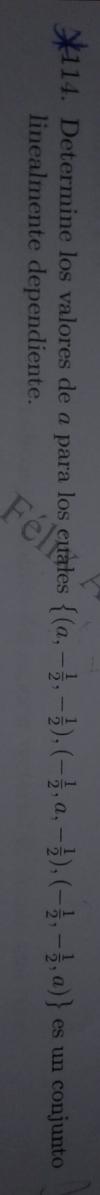-
Alex Domínguez
el 22/10/16 -
gemelo
el 22/10/16Buenas, quería ayuda a hayar el determinante de algunas matrices, lo que intento hacer en ellas es ''hacer ceros'' para simplificarlas pero no consigo dar con la clave. Dejo fotos:
-
lbp_14
el 22/10/16 -
jaime ignacio inostroza gonzalez
el 22/10/16que hago cuando tengo una inecuacion elevada a un exponente muy grande (x-3)^13 (x+3)^51(x-5)^100 ≥ 0 lo necesito saber
Matías Ignacio Loyola Galdames
el 22/10/16
Antonio Silvio Palmitano
el 22/10/16Recuerda que las expresiones con exponentes pares siempre toman valores mayores o iguales a cero, y que las expresiones con exponentes impares toman valores cuyos signos coinciden con los signos de sus bases.
Observa que el factor (x-5)^100 es positivo para todo valor de x, por lo que tienes dos opciones:
x - 3 >= 0 y x + 3 >= 0, que te conduce a: x >= 3 y x >= -3, que corresponde al subintervalo: [3,+inf);
x - 3 <= 0 y x + 3 <= 0, que te conduce a: x <= 3 y x <= -3, que corresponde al subinervalo: (-inf,-3].
Por lo tanto, el conjunto solución de la inecuación, expresado como intervalo, queda: S = (-inf,-3] u [3,+inf).
Espero haberte ayudado.
-
Manuel Ortiz
el 22/10/16
Buenos días, me podirán ayudaron dar algunas ideas para los siguientes problemas por favor, de antemano gracias.
David
el 24/10/16Se trata de que aportéis algo más que enunciados, sobre todo cuando son ejercicios universitarios (para los cuales debemos hacer excepciones en los foros pues unicoos por ahora se queda en bachiller). Si dejáis solo enunciados de 4 en 4, no os podemos ayudar. No se trata de que os hagamos los deberes.
En cualquier caso, se trata también de no colapsar los foros dejando fotos verticales...
Para el 114, simplemente discute el rango de la matriz en funcion de a... Si haces el determinante y lo igualas a cero, obtendrás los valores de "a" que hacen que el rango no sea 3, es decir, el valor de "a2 que hace que los vectores no sean independientes... Te sugiero los vídeos de "rango de una matriz" y los de "Rouche"...
En el primero, no se lo que te piden , el enunciado no tiene sentido... -
Pablo Reyes
el 22/10/16 -
Álvaro Grande Pérez
el 22/10/16¿Podría alguien discutir y resolverme este sistema por favor? Gracias.
David
el 24/10/16Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?
Echales un vistazo... Teorema de Rouche
-
Alicia
el 22/10/16Si sen x = 1/2 calcular,sin utilizar la calculadora.
tg(π-2x) y tg (π +2x)
Antonio Silvio Palmitano
el 22/10/16Debes tener en cuenta las identidades de adición para seno y coseno:
1) sen(pi-2x) = senpi*cos2x - cospi*sen2x = 0*cos2x - (-1)*sen2x = 0 + sen2x = 2senx*cosx (*).
cos(pi-2x) = cospi*cos2x + senpi*sen2x = -1*cos2x + 0*sen2x = - cos2x + 0 = - cos 2x = - ( (cosx)^2 - (senx)^2 ) = - (cosx)^2 + (senx)^2 (**).
Luego, a partir de la identidad fundamental podemos plantear:
(cosx)^2 = 1 - (senx)^2 = 1 - (1/2)^2 = 1 - 1/4 = 3/4, y luego: cosx = V(3/4) = V(3) / V(4) = V(3)/2.
Luego, la identidad señalada (*) queda: sen(pi-2x) =2*(1/2)*V(3)/2 = V(3)/2, y
la identidad señalada (**) queda: cos(pi-2x) = - ( V(3)/2 )^2 + (1/2)^2 = - 3/4 + 1/4 = -1/2.
Por último, planteamos la identidad trigonométrica para la tangente y queda:
tan(pi-2x) = sen(pi-2x) / cos(pi-2x) = (V(3)/2) / (-1/2) = - V(3).
2) Puedes hacer un trabajo similar a partir de las identidades:
sen(pi+2x) = senpi*cos2x - cospi*sen2x = continúa ...
cos(pi+2x) = cospi*cos2x - senpi*sen2x = continúa ...
Espero haberte ayudado.
-
Nenúfar
el 22/10/16Hola Unicoos:
Os dejo un problema de espacios vectoriales que no me sale.Me gustaría que me dijerais cual ha sido mi fallo y si mi razonamiento es correcto o no.
Antonio Silvio Palmitano
el 22/10/16Has resuelto bien el inciso (a).
Observa que no has copiado correctamente la expresión del polinomio p(x), pues has cambiado signo en el término lineal y en el término independiente.
Observa que la matriz inicial queda:
< 0 1 1 4 >
< 1 1 0 -1 >
< 1 0 1 2 >
Luego ensaya las operaciones elementales:
1° paso: permutación entre fila 1 y fila 2
2° paso: (fila 3 - fila 1)
3° paso: (fila 1 - fila 2) y (fila 3 - fila 2)
4° paso: (1/2)fila 3
5° paso: (fila 1 + fila 3) y (fila 2 - fila 3).
Espero haberte ayudado.
-
Alicia
el 22/10/16Hola. Alguien que sepa resolver esta ecuación?
cos2x - sen2x = 1
Alicia
el 22/10/16
