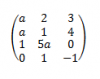-
Joship
el 21/10/16hola unicoos tengo un problema con este ejercicio no me resulta si alguien me hecha un mano por favor
-
Ruth Diaz
el 21/10/16Tengo una duda, cómo debería realizar esta operación?
-
Víctor Miranda
el 21/10/16- Por favor que alguien me ayude con estos dos ejercicios
- 1- Se extraen dos bolas de una urna con 8 bolas negras y 3 bolas blancas. a) cuál es la probabilidad de que las 2 sean negras? b) y de que sean ambas de color blanco? c) y de que sean de distinto color?
- 2- cuál es la probabilidad de que haya en un puñado de 6 cartas de una baraja de 48 cartas haya dos reyes? y de que haya dos o más Reyes?
Antonio Silvio Palmitano
el 21/10/16Vamos con orientaciones (indicamos número combinatorio con C):
1) Puedes hacer C(11,2) = 55 extracciones de dos bolillas, de un total de once que hay en la urna.
a) Puedes hacer C(8,2) = 28 extracciones de dos bolillas negras, luego: p =C(8,2) / C(11,2) = 28/55.
b) Puedes hacer C(3,2) = 3 extracciones de dos bolillas blancas, luego: p = C(3,2) / C(11,2) = 3/55.
c) Puedes hacer C(8,1)*C(3,1) = 8*3 = 24 extracciones de dos bolillas con una de cada color, luego: p = C(8,1)*C(3,1) / C(11,2) = 24/55.
Hemos considerado en todos los casos extracciones sin orden.
2) Puedes barajar C(48,6) manos distintas de seis cartas con una baraja de cuarenta y ocho cartas.
a) Puedes hacer C(4,2)*C(44,4) elecciones de dos reyes y otras cuatro cartas que no son reyes para cada mano,, luego: p = C(4,2)*C(44,4) / C(48,6).
b) La probabilidad será la suma de la probabilidad que hemos calculado en el ejercicio anterior (p), más la de tener tres reyes y otras tres cartas que no son reyes en la mano (q), más la de tener a los cuatro reyes y dos cartas que no son reyes en la mano (r). Luego tenemos:
p + q + r = C(4,2)*C(44,4) / C(48,6) + C(4,3)*C(44,3) / C(48,6) + C(4,4)*C(44,2) / C(44,6).
En todos los casos hemos considerado que las cartas se extraen de la baraja sin orden.
Espero haberta ayudado.
-
Albus99
el 21/10/16Hola, me ayudais a calcular el rango de esta matriz, no es cuadrada y no se como se haría
Antonio Silvio Palmitano
el 21/10/16Recuerda que el rango de una matriz es menor o igual al mínimo entre la cantidad de filas y la cantidad de columnas de la matriz. Por lo tanto, para este ejercicio tienes que el rango es menor o igual que tres.
Luego puedes tomar una submatriz cuadrada, por ejemplo con las tres primeras filas (observa que la cuarta fila es la resta entre las dos primeras filas, por lo que no la tomamos en cuenta).
Luego, desarrollas el determinante (D) de la submatriz y queda:
D = 5 - 5a^2.
Luego tenemos:
1) Si D es distinto de cero, a lo que corresponde: a distinto de -1 y a distinto de 1, el rango de la matriz será 3.
2) Si a = -1 (que corresponde a que el rango no es 3), reemplazas en la matriz original y puedes seleccionar una submatriz (por ejemplo, con los dos primeros elementos de las dos últimas filas), calculas su determinante (E) y queda:
E = 1 que es distinto de cero, por lo que tenemos que el rango será 2, para a = -1.
3) Si a = 1 (que corresponde a que el rano no es 3), reemplazas en la matriz original y puedes seleccionar una submatriz (por ejemplo con los dos primeros elementos de las dos primeras filas), calculas su determinante (F) y queda:
F = -1 que es distinto de cero, por lo que tenemos que el rango será 2, para a = 1.
Por lo tanto, concluimos que el rango de la matiriz es igual a:
3, si a es distinto de -1 y también a es distinto de 1,
2 si a es igual a -1 o a es igual a 1.
Espero haberte ayudado.
-
Ramón
el 21/10/16Tengo una duda de teoría de Espacios Vectoriales:
Se que hay pocos vídeos de ello aquí en únicos porque es nivel universidad y es una excepción, pero por si algún Unicoos se ve inspirado:
Se que para ser Base de un espacio vectorial tiene que ser Linealmente Independiente y Conjunto de generadores (Como bien se explica en un video de Unicoos), pero mi duda son los requisitos para ser Conjunto de Generadores, por lo que he leído en mi libro un conjunto de generadores puede no ser base, porque puede ser linealmente dependiente entre sí, entonces ¿como se si es un conjunto de generadores?
Debido a que si encuentro un x1 y un x2 que al multiplicarlo por 2 vectores de un espacio vectorial me da un vector generico (a,b,c), es generador porque he conseguido poner un vector genérico como combinación lineal de esos otros 2.
¡¡¿¿Pero necesito ver un ejemplo en el que desde unos vectores los que sean no se pueda expresar como combinación lineal de un vector genérico??!!
Si alguien pudiera explicarme de forma concisa cuales son las normas para que un conjunto sea generador en un espacio vectorial... Se lo agradecería eternamente...
Antonio Silvio Palmitano
el 21/10/16Vamos con algunas precisiones: una Base es un Conjunto Generador que tiene la mínima cantidad de vectores, todos linealmente independientes.
Un Conjunto Generador a secas, es todo conjunto que incluye una Base.y, observa que los vectores de la base incluida son independientes entre si, pero los vectores "excedentes" son todos combinaciones lineales de los vectores de la base incluida.
Vamos con un ejemplo, para fijar ideas:
Bc = { <1,0,0> , <0,1,0> , < 0,0,1> } es la base canónica del espacio vectorial R^3, y sus vectores son linealmente independientes, y Bc genera a R^3.
B = { <1,0,0> , <0,1,0> , < 0,0,1> , <1,1,0> , <0,1,2> } es un conjunto generador del espacio vectorial R^3 porque contiene a una base (en este ejemplo señalamos a la base canónica) de R^3).
Espero haberte ayudado.
-
Sebastian
el 21/10/16Muy buenos dias, me podrían ayudar con el ejercicio b? No se por donde cogerlo. Muchas gracias!
Ramón
el 21/10/16A ver Sebastian creo que la solución del ejercicio es encontrar un x1 y un x2 que multiplicados por los vectores u1 y u2 nos de el vector t. De esta forma tendrás el verctor t(a,b,c) como combinación lineal de u1 y u2.
x1·(u1)+x2·(u2)=(t) --> x1·(u1)+x2·(u2)=(a,b,c) --> simpre que x1 y x2 pertenezcan a los reales, esa sería la forma de expresarlos como combinación lineal del vector t que pertenece a R3.
Espero haberte ayudado y que esa fuera tu duda.
Ramón
el 21/10/16 -
Maria CR
el 21/10/16Hola, me podeis ayudar? Estoy practicando la racionalización de radicales.. como se racionalizaría por ejemplo:
-1/√5-2
Yo lo he hecho así pero creo que me falta poner el bien el numerador, no?
-1 = (-1)(√5+2) = (-1)(√5+2) = (-1)(√5+2) = (-1)(√5+2)
________ _____________ ____________ _____________
√5 - 2 (√5-2) (√5+2) √52-22 1
Antonio Silvio Palmitano
el 21/10/16
Ángel
el 24/10/16Creo que ha habido una gran confusión con lo de culipard@...
Al ver el nickname "Maria CR" y ver que era de España se me pasó por la cabeza que podría ser paisana mía, pues soy de Ciudad Real (CR)...a los de Ciudad Real nos llaman "culipardos"
http://elsayon.blogspot.com.es/2013/07/culipardo_24.html
Mis más sinceras disculpas a MariaCR, David... por emplear este término, que al ser desconocido para vosotros pudo parecer ofensivo!...pero ya digo, nada más lejos de la realidad fue un saludo totalmente sin ninguna intención. Sólo lo hice porque Ciudad Real al ser tan pequeño me pareció una casualidad encontrarme a alguien de allí por aquí
Buen día
-
Daniela
el 21/10/16hola unicos me pueden ayudar con este ejercicio
Determine el area de la region limitada por las graficas de las ecuaciones dadas :
y=x2 ; y2=x; 4x+3y-12= 0 &(x=0 o y=0)
-
Sofía
el 21/10/16
Hola unicoos! Me pueden ayudar con este ejercicio? Gracias.
En una prueba de tiro al blanco móvil con fusil, un competidor en reposo apunta al objetivo que se ubica a 180,00 m de distancia medida en horizontal y que se encuentra en movimiento normal al eje del fusil con una rapidez de 3,50 m / s. Siendo la rapidez de la bala de 140,00 m / s, determinar: a) el ángulo medido en horizontal que deberá existir entre la dirección del fusil y la del objetivo.
b) a cuantos metros por delante del objetivo debe apuntar el competidor para hacer blanco.-
-
Estefany Guevara
el 21/10/16
